题目内容
(本小题满分15分)设 ,
, .
.
(1)当 时,求曲线
时,求曲线 在
在 处的切线的斜率;
处的切线的斜率;
(2)如果存在 ,使得
,使得 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数 ;
;
(3)如果对于任意 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 ,
, .
.(1)当
 时,求曲线
时,求曲线 在
在 处的切线的斜率;
处的切线的斜率;(2)如果存在
 ,使得
,使得 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数 ;
;(3)如果对于任意
 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.(1)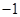 (2)
(2)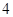 (3)
(3)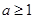
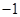 (2)
(2)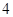 (3)
(3)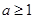
试题分析:(1)当
 时,
时,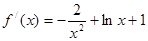 ,故
,故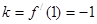 . ……3分
. ……3分(2)存在
 ,使得
,使得 成立等价于
成立等价于 ,
,∵
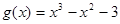 ,∴
,∴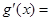
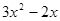 ,
,∴
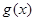 在
在 上单调递减,在
上单调递减,在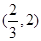 上单调递增, ……6分
上单调递增, ……6分∴
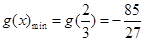 ,
,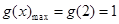 ,
,∴
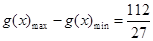 ,
, ∴满足的最大整数
 为4; ……8分
为4; ……8分(3)对于任意
 ,都有
,都有 成立,等价于
成立,等价于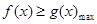 .
.由(2)知,在
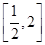 上,
上,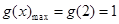 ,
,∴在
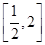 上,
上,
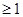 恒成立,等价于
恒成立,等价于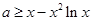 恒成立,
恒成立,记
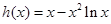 ,则
,则 且
且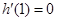 ,
,∴当
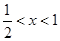 时,
时,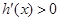 ;当
;当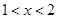 时,
时,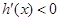 ,
,∴函数
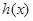 在
在 上单调递增,在
上单调递增,在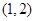 上单调递减,
上单调递减,∴
 ∴
∴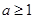 . ……15分
. ……15分合运算所学知识分析问题、解决问题的能力和运算求解能力.
点评:恒成立问题是高考中一个常考的考点,恒成立问题一般转化成最值问题来解决.导数是研究函数性
质尤其是单调性、最值问题的有力工具,要灵活运算,但是不要忘记定义域.

练习册系列答案
相关题目
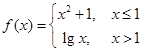 ,则
,则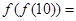 _______________.
_______________.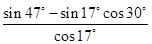 =____________.
=____________. ;
;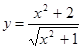 ;②
;②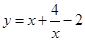 ;③
;③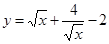 ;④
;④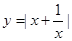 ;⑤
;⑤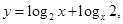 其中
其中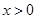 且
且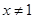 ;⑥
;⑥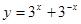 .其中最小值为2的函数是 (填入序号 ).
.其中最小值为2的函数是 (填入序号 ).



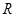 上的函数
上的函数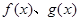 满足
满足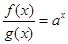 ,且
,且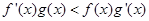
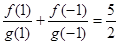 ,若有穷数列
,若有穷数列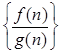 (
(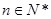 )的前
)的前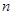 项和等于
项和等于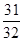 ,则
,则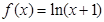 满足0<
满足0<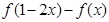 <1。
<1。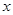 的取值范围;
的取值范围;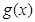 是偶函数且满足
是偶函数且满足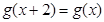 ,当
,当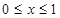 时,有
时,有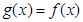 ,求
,求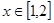 上的解析式。
上的解析式。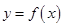 是定义在
是定义在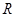 上的奇函数,且当
上的奇函数,且当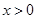 时不等式
时不等式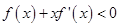 成立,若
成立,若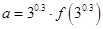 ,
, 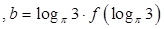
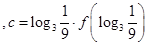 ,则
,则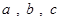 大小关系是( )
大小关系是( )



 的图象经过点
的图象经过点 ,则
,则 .
.