题目内容
【题目】甲、乙两人各掷一个均匀的骰子，观察朝上的面的点数，记事件A：甲得到的点数为2，B：乙得到的点数为奇数.
（1）求
，
，
，判断事件A与B是否相互独立；
（2）求
.
【答案】（1）
，
，
，A与B相互独立；（2）
.
【解析】
（1）根据古典槪型的概率公式计算可得
，
，
，再根据
可判断出A与B是相互独立的.
（2）由A与B相互独立可知，
与B也相互独立，再根据相互独立事件的乘法公式可得.
解：如果用
表示甲得到的点数为i，乙得到的点数为j，则样本空间可以记为
，
而且这个样本空间可用图直观表示.
（1）不难看出，图中，A框中的点代表事件
框中的点代表事件B.
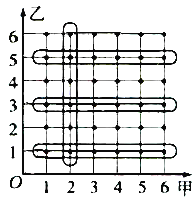
因此，可以算出
，
.
又因为
，所以
.
因为，所以A与B相互独立.
（2）由A与B相互独立可知，与B也相互独立，
因此
.
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
【题目】某高三理科班共有60名同学参加某次考试，从中随机挑选出5名同学，他们的数学成绩
与物理成绩
如下表：
数学成绩 | 145 | 130 | 120 | 105 | 100 |
物理成绩 | 110 | 90 | 102 | 78 | 70 |
数据表明与之间有较强的线性关系．
（I）求关于的线性回归方程；
（II）该班一名同学的数学成绩为110分，利用（I）中的回归方程，估计该同学的物理成绩；
（III）本次考试中，规定数学成绩达到125分为优秀，物理成绩达到100分为优秀. 若
该班数学优秀率与物理优秀率分别为50%和60%，且除去抽走的5名同学外，剩下的同学中数学优秀但物理不优秀的同学共有5人，在答卷页上填写下面2×2列联表，判断能否在犯错误的概率不超过0.01的前提下认为数学优秀与物理优秀有关？
物理优秀 | 物理不优秀 | 合计 | |
数学优秀 | |||
数学不优秀 | |||
合计 | 60 |
参考数据：回归直线的系数
，
，
