题目内容
【题目】在平面直角坐标系中,已知两定点![]() 、
、![]() ,⊙C的方程为
,⊙C的方程为![]() .当⊙C的半径取最小值时:
.当⊙C的半径取最小值时:
(1)求出此时m的值,并写出⊙C的标准方程;
(2)在x轴上是否存在异于点E的另外一个点F,使得对于⊙C上任意一点P,总有![]() 为定值?若存在,求出点F的坐标,若不存在,请说明你的理由;
为定值?若存在,求出点F的坐标,若不存在,请说明你的理由;
(3)在第(2)问的条件下,求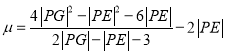 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)把一般方程化为标注形式,由二次函数最值得![]() ;(2)由于λ取值与x无关,则对应项系数成比例;(3) 在第(2)问的条件下,
;(2)由于λ取值与x无关,则对应项系数成比例;(3) 在第(2)问的条件下, ![]() ,利用对勾函数求最值.
,利用对勾函数求最值.
试题解析:
(1)⊙C的标准式为: ![]() ,
,
当![]() 时,⊙C的半径取最小值,此时⊙C的标准方程为
时,⊙C的半径取最小值,此时⊙C的标准方程为![]() ;
;
(2)设![]() ,定点
,定点![]() (m为常数),则
(m为常数),则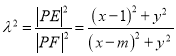 .
.
∵![]() ,∴
,∴![]() ,代入上式,
,代入上式,
得: 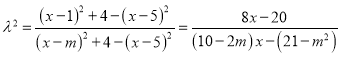 .
.
由于λ取值与x无关,∴![]() (
(![]() 舍去).
舍去).
此时点F的坐标为![]() ,
, ![]() 即
即![]() ;
;
(3)
由上问可知对于⊙C上任意一点P总有![]() ,
,
故![]() ,
,
而![]() (当P、F、G三点共线时取等号),
(当P、F、G三点共线时取等号),
又![]() ,故
,故![]() .
.
∴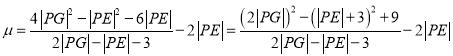
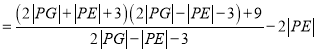
![]() ,
,
令![]() ,则
,则![]() ,
,
根据对勾函数的单调性可得: ![]() .
.

练习册系列答案
相关题目