题目内容
7.对于函数f(x)定义域中任意的x1,x2(x1≠x2)有如下结论①f(x1+x2)=f(x1)•f(x2)
②f(x1•x2)=f(x1)+f(x2)
③$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0
④f($\frac{{x}_{1}+{x}_{2}}{2}$)<$\frac{f({x}_{1})+f({x}_{2})}{2}$
当f(x)=log${\;}_{\frac{1}{2}}$x时,上述结论中正确的序号是( )
| A. | ①③ | B. | ②③ | C. | ②④ | D. | ②③④ |
分析 结合对数的运算性质及对数函数的图象和性质,逐一分析四个结论的真假,可得答案.
解答 解:当f(x)=log${\;}_{\frac{1}{2}}$x时,
①f(x1+x2)=f(x1)•f(x2) 不一定成立,故错误;
②f(x1•x2)=f(x1)+f(x2)一定成立,故正确;
③函数为减函数,故$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0一定成立,故正确;
④函数凹函数,故f($\frac{{x}_{1}+{x}_{2}}{2}$)<$\frac{f({x}_{1})+f({x}_{2})}{2}$一定成立,故正确;
故正确的命题的序号是②③④,
故选:D
点评 本题考查的知识点是对数的运算性质及对数函数的图象和性质,难度中档.

练习册系列答案
相关题目
12.函数y=x2-x+2在[a,+∞)上单调递增是函数y=ax为单调递增函数的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
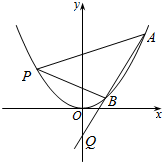 已知抛物线C:x2=4y的焦点为F,O为坐标原点,过Q(0,m)作直线交抛物线C于A,B两点,点P在抛物线C上,且满足$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FP}$=$\overrightarrow{0}$.
已知抛物线C:x2=4y的焦点为F,O为坐标原点,过Q(0,m)作直线交抛物线C于A,B两点,点P在抛物线C上,且满足$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FP}$=$\overrightarrow{0}$.