题目内容
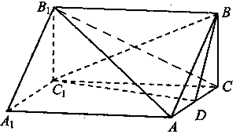
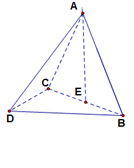
(本题满分14分)如图,三棱柱ABC—A1B1C1中,AA1 面ABC,BC
面ABC,BC AC,BC=AC=2,D为AC的中点。
AC,BC=AC=2,D为AC的中点。
(1)若AA1=2,求证: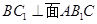 ;
;
(2)若AA1=3,求二面角C1—BD—C的余弦值.
 面ABC,BC
面ABC,BC AC,BC=AC=2,D为AC的中点。
AC,BC=AC=2,D为AC的中点。
(1)若AA1=2,求证:
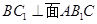 ;
;(2)若AA1=3,求二面角C1—BD—C的余弦值.
(1)见解析;(2)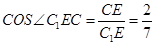 .
.
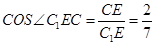 .
.本试题主要是考查了线面垂直的证明,以及二面角的求解的综合运用
(1)因为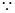 AA1= BC=2.
AA1= BC=2.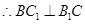 , 又AA1
, 又AA1 面ABC,关键是求证AC
面ABC,关键是求证AC 面B C1,从而得到线面垂直的证明。,
面B C1,从而得到线面垂直的证明。,
(2)利用三垂线定理,先作出二面角,然后借助于三角形的边角的关系得到结论。
(1)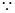 AA1= BC=2.
AA1= BC=2.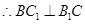 , 又AA1
, 又AA1 面ABC,
面ABC,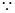
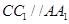 ,
, CC1
CC1 ABC,
ABC,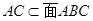 , CC1
, CC1 AC ,而BC
AC ,而BC AC,CC1
AC,CC1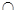 BC=C
BC=C AC
AC 面B C1,
面B C1,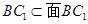 .
.
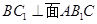 . --------(7分)
. --------(7分)
(2)过点C作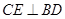 于点E,连接
于点E,连接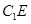 ,
, CC1
CC1 面ABC,
面ABC,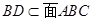 , CC1
, CC1 BD, 又
BD, 又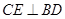 ,CC1
,CC1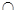 EC=C,
EC=C,
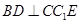 ,
,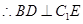 .故
.故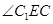 为二面角C1—BD—C的平面角。BC=2,CC1=3,
为二面角C1—BD—C的平面角。BC=2,CC1=3,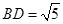 ,
,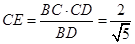 .在直角三角形
.在直角三角形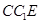 中,CC1=3,
中,CC1=3,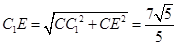 .
. 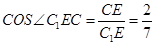 .-------------(14分)
.-------------(14分)
(1)因为
 AA1= BC=2.
AA1= BC=2.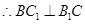 , 又AA1
, 又AA1 面ABC,关键是求证AC
面ABC,关键是求证AC 面B C1,从而得到线面垂直的证明。,
面B C1,从而得到线面垂直的证明。,(2)利用三垂线定理,先作出二面角,然后借助于三角形的边角的关系得到结论。
(1)
 AA1= BC=2.
AA1= BC=2.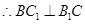 , 又AA1
, 又AA1 面ABC,
面ABC,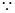
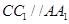 ,
, CC1
CC1 ABC,
ABC,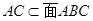 , CC1
, CC1 AC ,而BC
AC ,而BC AC,CC1
AC,CC1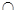 BC=C
BC=C AC
AC 面B C1,
面B C1,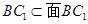 .
.
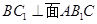 . --------(7分)
. --------(7分)(2)过点C作
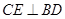 于点E,连接
于点E,连接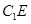 ,
, CC1
CC1 面ABC,
面ABC,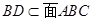 , CC1
, CC1 BD, 又
BD, 又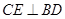 ,CC1
,CC1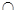 EC=C,
EC=C,
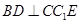 ,
,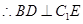 .故
.故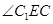 为二面角C1—BD—C的平面角。BC=2,CC1=3,
为二面角C1—BD—C的平面角。BC=2,CC1=3,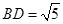 ,
,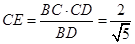 .在直角三角形
.在直角三角形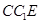 中,CC1=3,
中,CC1=3,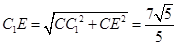 .
. 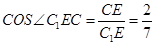 .-------------(14分)
.-------------(14分)
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
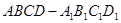 ,
, 是底
是底 对角线的交点.
对角线的交点.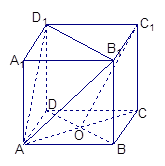
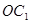 ∥面
∥面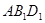 ;(2)
;(2)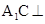 面
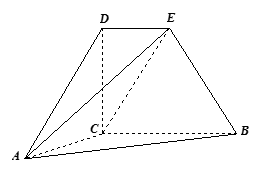
面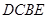 为直角梯形,
为直角梯形,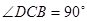 ,
,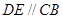 ,
,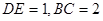 ,又
,又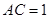 ,
,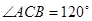 ,
,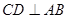 ,直线
,直线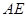 与直线
与直线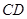 所成角为
所成角为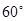 .
.
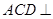 平面
平面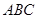 ;
;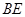 与平面
与平面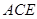 所成角的正弦值.
所成角的正弦值.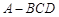 中,
中, 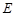 是
是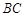 的中点,
的中点,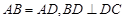
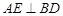 ;
;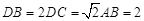 ,且二面角
,且二面角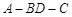 为
为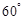 ,求
,求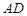 与面
与面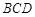 所成角的正弦值。
所成角的正弦值。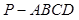 的底面
的底面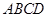 是正方形,侧棱
是正方形,侧棱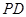 ⊥底面
⊥底面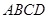 ,
,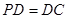 ,
,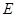 是
是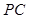 的中点.
的中点. 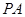 //平面
//平面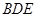 ;
; 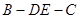 的平面角的余弦值;
的平面角的余弦值;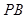 上是否存在点
上是否存在点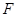 ,使
,使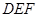 ?若存在,请求出
?若存在,请求出 是等腰梯形,
是等腰梯形, ∥
∥ ,
,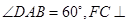 平面
平面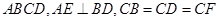 .
.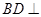 平面
平面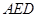 ;
;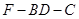 的余弦值.
的余弦值.
 的底面边长为
的底面边长为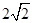 ,
,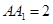 ,点
,点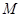 是
是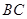 的中点,
的中点,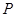 是平面
是平面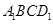 内的一个动点,且满足
内的一个动点,且满足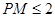 ,
,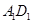 和
和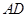 的距离相等,则点
的距离相等,则点
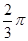
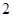
 ,
, 是不同的平面,
是不同的平面, ,
, 是不同的直线,给出下列命题:
是不同的直线,给出下列命题: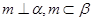 ,则
,则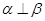 ;
;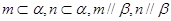 ,则
,则 ;
;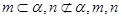 是异面直线,则
是异面直线,则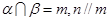 ,且
,且 ,则
,则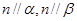 .
.