题目内容
设函数f(x)的定义域为D,如果存在正实数k,使对任意x∈D,都有x+k∈D,且f(x+k)>f(x)恒成立,则称函数f(x)在D上的“k阶增函数”.已知f(x)是定义在R上的奇函数,且当x>0时,x>0时,f(x)=|x-a|-a,其中a为正常数,若f(x)为R上的“2阶增函数”,则实数a的取值范围是( )
A.(0,2)
B.(0,1)
C.(0,
 )
)D.(0,
 )
)
【答案】分析:由题意可以得到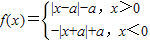 ,再由定义存在正实数k,使对任意x∈D,都有x+k∈D,且f(x+k)>f(x)恒成立,则称函数f(x)为D上的“k阶增函数”.对所给的问题分自变量全为正,全为负,一正一负三类讨论,求出参数所满足的共同范围即可.
,再由定义存在正实数k,使对任意x∈D,都有x+k∈D,且f(x+k)>f(x)恒成立,则称函数f(x)为D上的“k阶增函数”.对所给的问题分自变量全为正,全为负,一正一负三类讨论,求出参数所满足的共同范围即可.
解答:解:∵f(x)是定义在R上的奇函数,
且当x>0时,f(x)=|x-a|-a,
∴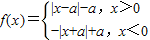 ,
,
又f(x)为R上的“2阶增函数”,
当x>0时,由定义有|x+2-a|-a>|x-a|-a,
即|x+2-a|>|x-a|,其几何意义为到点a小于到点a-2的距离,
由于x>0故可知a+a-2<0得a<1.
当x<0时,分两类研究:
①若x+2<0,则有-|x+2+a|+a>-|x+a|+a,
即|x+a|>|x+2+a|,其几何意义表示到点-a的距离小于到点-a-2的距离,
由于x<0,故可得-a-a-2>0,得a<-1;
②若x+2>0,则有|x+2-a|-a>-|x+a|+a,
即|x+a|+|x+2-a|>2a,其几何意义表示到到点-a的距离与到点a-2的距离的和大于2a,
当a≤0时,显然成立,
当a>0时,由于|x+a|+|x+2-a|≥|-a-a+2|=|2a-2|,
故有|2a-2|>2a,必有2-2a>2a,解得 ,
,
综上,对x∈R都成立的实数a的取值范围是a< .
.
故选C.
点评:本题考查奇偶性与单调性的综合,解题的关键是根据函数的奇函数的性质求出函数的解析式,理解本题中所给的定义,以及根据函数解析式对问题分为三部分来求解,最后求出三部分中的公共部分的取值范围作为实数a的取值范围是本题中的一个疑点,也是易错点,一般分类求解都是求并集,而本题因为是研究的定义域各个部分上成立的参数的范围,故在整个定义域上都成立的参数的范围应该是三部分中都成立的范围的公共部分,对此逻辑关系一定要理解清楚.题后可以找一些分类讨论的题对比着题设条件好好理解领会一下.
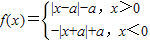 ,再由定义存在正实数k,使对任意x∈D,都有x+k∈D,且f(x+k)>f(x)恒成立,则称函数f(x)为D上的“k阶增函数”.对所给的问题分自变量全为正,全为负,一正一负三类讨论,求出参数所满足的共同范围即可.
,再由定义存在正实数k,使对任意x∈D,都有x+k∈D,且f(x+k)>f(x)恒成立,则称函数f(x)为D上的“k阶增函数”.对所给的问题分自变量全为正,全为负,一正一负三类讨论,求出参数所满足的共同范围即可.解答:解:∵f(x)是定义在R上的奇函数,
且当x>0时,f(x)=|x-a|-a,
∴
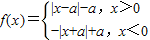 ,
,又f(x)为R上的“2阶增函数”,
当x>0时,由定义有|x+2-a|-a>|x-a|-a,
即|x+2-a|>|x-a|,其几何意义为到点a小于到点a-2的距离,
由于x>0故可知a+a-2<0得a<1.
当x<0时,分两类研究:
①若x+2<0,则有-|x+2+a|+a>-|x+a|+a,
即|x+a|>|x+2+a|,其几何意义表示到点-a的距离小于到点-a-2的距离,
由于x<0,故可得-a-a-2>0,得a<-1;
②若x+2>0,则有|x+2-a|-a>-|x+a|+a,
即|x+a|+|x+2-a|>2a,其几何意义表示到到点-a的距离与到点a-2的距离的和大于2a,
当a≤0时,显然成立,
当a>0时,由于|x+a|+|x+2-a|≥|-a-a+2|=|2a-2|,
故有|2a-2|>2a,必有2-2a>2a,解得
 ,
,综上,对x∈R都成立的实数a的取值范围是a<
 .
.故选C.
点评:本题考查奇偶性与单调性的综合,解题的关键是根据函数的奇函数的性质求出函数的解析式,理解本题中所给的定义,以及根据函数解析式对问题分为三部分来求解,最后求出三部分中的公共部分的取值范围作为实数a的取值范围是本题中的一个疑点,也是易错点,一般分类求解都是求并集,而本题因为是研究的定义域各个部分上成立的参数的范围,故在整个定义域上都成立的参数的范围应该是三部分中都成立的范围的公共部分,对此逻辑关系一定要理解清楚.题后可以找一些分类讨论的题对比着题设条件好好理解领会一下.

练习册系列答案
相关题目
 )与b=f(
)与b=f( )的大小关系为________.
)的大小关系为________. )与b=f(
)与b=f( )的大小关系为 .
)的大小关系为 . )与b=f(
)与b=f( )的大小关系为( ).
)的大小关系为( ).