题目内容
【题目】已知椭圆C的方程为![]() ,
,![]() 为椭圆C的左右焦点,离心率为
为椭圆C的左右焦点,离心率为![]() ,短轴长为2。
,短轴长为2。
(1)求椭圆C的方程;
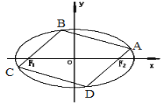
(2)如图,椭圆C的内接平行四边形ABCD的一组对边分别过椭圆的焦点![]() ,求该平行四边形ABCD面积的最大值.
,求该平行四边形ABCD面积的最大值.
【答案】(1) ![]() (2) 2
(2) 2![]()
【解析】
(1)由题意可得2b=2,结合椭圆的离心率,求得![]() 的值,得到椭圆的方程;
的值,得到椭圆的方程;
(2)求出直线AD与![]() 轴垂直时平行四边形ABCD面积的值为
轴垂直时平行四边形ABCD面积的值为![]() ,再设出AD所在直线斜率存在时的直线方程,联立直线方程和椭圆方程,求出AD的长度,再求出两平行线间的距离,代入平行四边形面积公式,可得平行四边形ABCD面积小于
,再设出AD所在直线斜率存在时的直线方程,联立直线方程和椭圆方程,求出AD的长度,再求出两平行线间的距离,代入平行四边形面积公式,可得平行四边形ABCD面积小于![]() ,从而求得结果.
,从而求得结果.
(1)依题意得2b=2,![]() ,解得
,解得![]() ,
,
所以椭圆C的方程为![]() 。
。
(2)当AD所在直线与![]() 轴垂直时,则AD所在直线方程为x=1,
轴垂直时,则AD所在直线方程为x=1,
联立![]() ,解得y=
,解得y=![]() ,
,
此时平行四边形ABCD的面积S=2![]() ;
;
当AD所在的直线斜率存在时,设直线方程为y=k(x-1),
联立![]() ,得
,得![]() ,
,
设A(![]() )D(
)D(![]() ),则
),则![]() ,
,
则 ,
,
两条平行线间的距离![]() ,则平行四边形ABCD的面积
,则平行四边形ABCD的面积 ,
,
令t=![]() ,
,
则S= ,
,![]() ,
,
开口向下,关于![]() 单调递减,则
单调递减,则![]() ,
,
综上所述,平行四边形ABCD的面积的最大值为![]() 。
。

【题目】![]() 年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分
年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分![]() 分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 不低于90分 |
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有![]() 人.
人.
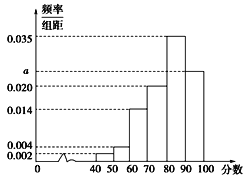
(1)求频率分布于直方图中![]() 的值,及评分等级不满意的人数;
的值,及评分等级不满意的人数;
(2)相关部门对项目进行验收,验收的硬性指标是:市民对该项目的满意指数不低于![]() ,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.
,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.
【题目】某校高三4班有50名学生进行了一场投篮测试,其中男生30人,女生20人.为了了解其投篮成绩,甲、乙两人分别都对全班的学生进行编号(1-50号),并以不同的方法进行数据抽样,其中一人用的是系统抽样,另一人用的是分层抽样.若此次投篮测试的成绩大于或等于80分视为优秀,小于80分视为不优秀,以下是甲、乙两人分别抽取的样本数据:
甲抽取的样本数据
编号 | 2 | 7 | 12 | 17 | 22 | 27 | 32 | 37 | 42 | 47 |
性别 | 男 | 女 | 男 | 男 | 女 | 男 | 女 | 男 | 女 | 女 |
投篮成 绩 | 90 | 60 | 75 | 80 | 83 | 85 | 75 | 80 | 70 | 60 |
乙抽取的样本数据
编号 | 1 | 8 | 10 | 20 | 23 | 28 | 33 | 35 | 43 | 48 |
性别 | 男 | 男 | 男 | 男 | 男 | 男 | 女 | 女 | 女 | 女 |
投篮成 绩 | 95 | 85 | 85 | 70 | 70 | 80 | 60 | 65 | 70 | 60 |
(Ⅰ)在乙抽取的样本中任取3人,记投篮优秀的学生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
(Ⅱ)请你根据乙抽取的样本数据完成下列2×2列联表,判断是否有95%以上的把握认为投篮成绩和性别有关?
优秀 | 非优秀 | 合计 | |
男 | |||
女 | |||
合计 | 10 |
(Ⅲ)判断甲、乙各用何种抽样方法,并根据(Ⅱ)的结论判断哪种抽样方法更优?说明理由.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(参考公式: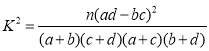 ,其中
,其中![]() )
)
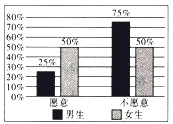
【题目】某组织在某市征集志愿者参加志愿活动,现随机抽出60名男生和40名女生共100人进行调查,统计出100名市民中愿意参加志愿活动和不愿意参加志愿活动的男女生比例情况,具体数据如图所示.
(1)根据条件完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为愿意参与志愿活动与性别有关?
的把握认为愿意参与志愿活动与性别有关?
愿意 | 不愿意 | 总计 | |
男生 | |||
女生 | |||
总计 |
(2)现用分层抽样的方法从愿意参加志愿活动的市民中选取7名志愿者,再从中抽取2人作为队长,求抽取的2人至少有一名女生的概率.
参考数据及公式:
|
|
|
|
|
|
|
|
|
|
![]() .
.