题目内容
已知函数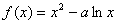 在
在 是增函数,
是增函数, 在
在 为减函数.
为减函数.
(1)求 ,
, 的表达式;
的表达式;
(2)求证:当 时,方程
时,方程 有唯一解;
有唯一解;
(3)当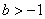 时,若
时,若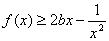 在
在 内恒成立,求
内恒成立,求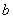 的取值范围.
的取值范围.
【答案】
解(1)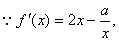 依题意
依题意 2分
2分
又∵ ,依题意
,依题意 ……………3分
……………3分

 ……………………………………4分
……………………………………4分
(2)由(1)可知,原方程为
设 …………………5分
…………………5分
令
令 ………………………………………7分
………………………………………7分
由
|
|
(0,1) |
1 |
(1,+∞) |
|
|
- |
0 |
+ |
|
|
递减 |
0 |
递增 |
即 在
在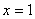 处有一个最小值0,即当
处有一个最小值0,即当 时,
时, >0,
>0, 只有一个解.
只有一个解.
即当x>0时,方程 有唯一解. ………………………………………8分
有唯一解. ………………………………………8分
(3) 当
当 时,
时,
 为减函数,其最小值为1.
………………………………………9分
为减函数,其最小值为1.
………………………………………9分
令 恒成立…………10分
恒成立…………10分
∴函数 在
在 为增函数,其最大值为2b-1,…………………11分
为增函数,其最大值为2b-1,…………………11分
依题意 ,解得
,解得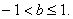 为所求范围. …………………………………12分
为所求范围. …………………………………12分

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目


 在
在 是增函数,则实数
是增函数,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D. 
 .
. 是增函数,当|m|最小时,求m的值.
是增函数,当|m|最小时,求m的值.