题目内容
已知函数f(x)和g(x)的图象关于点(1,1)对称,且f(x)=2x.(Ⅰ)求函数g(x)的解析式;
(Ⅱ)若h(x)=f(x)-λg(x)+2λ(λ>0)在[1,+∞)上是增函数,求实数λ的取值范围.
【答案】分析:(Ⅰ)设函数y=f(x)的图象上任意一点Q(x,y)关于点(1,1)的对称点为P(x,y),则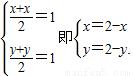 由点Q(x,y)在函数y=f(x)的图象上可得,
由点Q(x,y)在函数y=f(x)的图象上可得,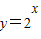 ,从而可求y=f(x)
,从而可求y=f(x)
(Ⅱ) 由(I)可得h(x)=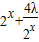 在[1,+∞)上是增函数,即可得当1≤x1<x2时,h(x2)-h(x1)>0,
在[1,+∞)上是增函数,即可得当1≤x1<x2时,h(x2)-h(x1)>0,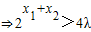 ,从而可求
,从而可求
解答:解:(Ⅰ)设函数y=f(x)的图象上任意一点Q(x,y)关于点(1,1)的对称点为P(x,y),则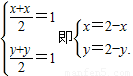 (4分)
(4分)
∵点Q(x,y)在函数y=f(x)的图象上,
∴2-y=22-x,即y=2-22-x,故g(x)=2-22-x.(6分)
(Ⅱ)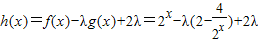 =
=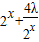 (7分)
(7分)
设1≤x1<x2,

=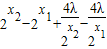 =
=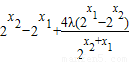
=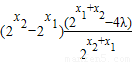 (10分)
(10分)
h(x)=f(x)-λg(x)+2λ(λ>0)在[1,+∞)上是增函数h(x2)-h(x1)>0,

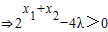 (12分)
(12分)
 ,∵x2>x1≥1,⇒x2+x1>2,
,∵x2>x1≥1,⇒x2+x1>2,
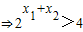 ,∴4≥4λ∴0<λ≤1为所求 (14分)
,∴4≥4λ∴0<λ≤1为所求 (14分)
点评:本题主要考查了关于点对称的函数的解析式的求解,主要利用的是中点坐标公式,函数的单调性的定义的应用及单调性中的恒成立的问题.
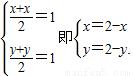 由点Q(x,y)在函数y=f(x)的图象上可得,
由点Q(x,y)在函数y=f(x)的图象上可得,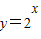 ,从而可求y=f(x)
,从而可求y=f(x)(Ⅱ) 由(I)可得h(x)=
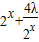 在[1,+∞)上是增函数,即可得当1≤x1<x2时,h(x2)-h(x1)>0,
在[1,+∞)上是增函数,即可得当1≤x1<x2时,h(x2)-h(x1)>0,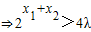 ,从而可求
,从而可求解答:解:(Ⅰ)设函数y=f(x)的图象上任意一点Q(x,y)关于点(1,1)的对称点为P(x,y),则
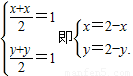 (4分)
(4分)∵点Q(x,y)在函数y=f(x)的图象上,

∴2-y=22-x,即y=2-22-x,故g(x)=2-22-x.(6分)
(Ⅱ)
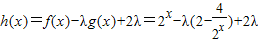 =
=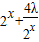 (7分)
(7分)设1≤x1<x2,


=
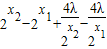 =
=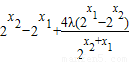
=
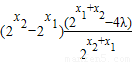 (10分)
(10分)h(x)=f(x)-λg(x)+2λ(λ>0)在[1,+∞)上是增函数h(x2)-h(x1)>0,

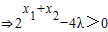 (12分)
(12分) ,∵x2>x1≥1,⇒x2+x1>2,
,∵x2>x1≥1,⇒x2+x1>2,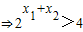 ,∴4≥4λ∴0<λ≤1为所求 (14分)
,∴4≥4λ∴0<λ≤1为所求 (14分)点评:本题主要考查了关于点对称的函数的解析式的求解,主要利用的是中点坐标公式,函数的单调性的定义的应用及单调性中的恒成立的问题.

练习册系列答案
相关题目