题目内容
已知函数 .
.(Ⅰ)求f(x)的最小正周期;
(Ⅱ)把f(x)的图象向右平移m个单位后,在
 是增函数,当|m|最小时,求m的值.
是增函数,当|m|最小时,求m的值.
【答案】分析:(Ⅰ)利用两角差的余弦公式与二倍角公式将f(x)=2cosxcos(x- )-
)-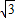 sin2x+sinxcosx化为f(x)=2sin(2x+
sin2x+sinxcosx化为f(x)=2sin(2x+ )及可求其周期;
)及可求其周期;
(Ⅱ)由f(x)=2sin(2x+ )的图象向右平移m个单位后,得到g(x)=2sin(2x-2m+),可求其单调增区间为[-
)的图象向右平移m个单位后,得到g(x)=2sin(2x-2m+),可求其单调增区间为[- +m+kπ,
+m+kπ, +m+kπ],再结合g(x)在
+m+kπ],再结合g(x)在 是增函数,即可求得|m|最小值.
是增函数,即可求得|m|最小值.
解答:解:( I)f(x)=2cosxcos(x- )-
)- sin2x+sinxcosx
sin2x+sinxcosx
=2cosx(cosxcos +sinxsin
+sinxsin )-
)- sin2x+sinxcosx
sin2x+sinxcosx
= cos2x+sinxcosx-
cos2x+sinxcosx- sin2x+sinxcosx
sin2x+sinxcosx
= (cos2x-sin2x)+2sinxcosx
(cos2x-sin2x)+2sinxcosx
=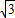 cos2x+sin2x
cos2x+sin2x
=2sin(2x+ )…(4分)
)…(4分)
∴T= =π…(6分)
=π…(6分)
(II)g(x)=2sin(2x-2m+ )…(8分)
)…(8分)
由2kπ- ≤2x-2m+
≤2x-2m+ ≤2kπ+
≤2kπ+ 得单调递增区间为[-
得单调递增区间为[- +m+kπ,
+m+kπ, +m+kπ],
+m+kπ],
∵g(x)在 是增函数,
是增函数,
∴- +m+kπ=0,m=
+m+kπ=0,m= -kπ,…(10分)
-kπ,…(10分)
∴当|m|最小时,m= …(12分)
…(12分)
点评:本题考查函数y=Asin(ωx+φ)的图象变换,综合考察了两角差的余弦公式与二倍角公式、辅助角公式的应用,考查了正弦函数的单调性,求最值问题等,熟练掌握三角函数公式与三角函数性质是解决问题的关键,属于难题.
 )-
)-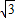 sin2x+sinxcosx化为f(x)=2sin(2x+
sin2x+sinxcosx化为f(x)=2sin(2x+ )及可求其周期;
)及可求其周期;(Ⅱ)由f(x)=2sin(2x+
 )的图象向右平移m个单位后,得到g(x)=2sin(2x-2m+),可求其单调增区间为[-
)的图象向右平移m个单位后,得到g(x)=2sin(2x-2m+),可求其单调增区间为[- +m+kπ,
+m+kπ, +m+kπ],再结合g(x)在
+m+kπ],再结合g(x)在 是增函数,即可求得|m|最小值.
是增函数,即可求得|m|最小值.解答:解:( I)f(x)=2cosxcos(x-
 )-
)- sin2x+sinxcosx
sin2x+sinxcosx=2cosx(cosxcos
 +sinxsin
+sinxsin )-
)- sin2x+sinxcosx
sin2x+sinxcosx=
 cos2x+sinxcosx-
cos2x+sinxcosx- sin2x+sinxcosx
sin2x+sinxcosx=
 (cos2x-sin2x)+2sinxcosx
(cos2x-sin2x)+2sinxcosx=
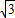 cos2x+sin2x
cos2x+sin2x=2sin(2x+
 )…(4分)
)…(4分)∴T=
 =π…(6分)
=π…(6分)(II)g(x)=2sin(2x-2m+
 )…(8分)
)…(8分)由2kπ-
 ≤2x-2m+
≤2x-2m+ ≤2kπ+
≤2kπ+ 得单调递增区间为[-
得单调递增区间为[- +m+kπ,
+m+kπ, +m+kπ],
+m+kπ],∵g(x)在
 是增函数,
是增函数,∴-
 +m+kπ=0,m=
+m+kπ=0,m= -kπ,…(10分)
-kπ,…(10分)∴当|m|最小时,m=
 …(12分)
…(12分)点评:本题考查函数y=Asin(ωx+φ)的图象变换,综合考察了两角差的余弦公式与二倍角公式、辅助角公式的应用,考查了正弦函数的单调性,求最值问题等,熟练掌握三角函数公式与三角函数性质是解决问题的关键,属于难题.

练习册系列答案
相关题目
 .
.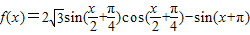 .
. 个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.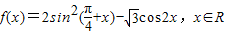 .
.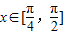 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.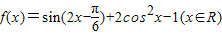 .
.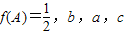 成等差数列,且
成等差数列,且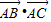 =9,求a的值.
=9,求a的值.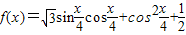 .
.