题目内容
若函数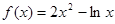 在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )
在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )
A. | B.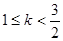 |
C.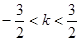 | D.不存在这样的实数k |
B
解析试题分析:根据题意,由于函数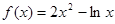 在其定义域内的一个子区间(k-1,k+1)内是单调函数,则可知
在其定义域内的一个子区间(k-1,k+1)内是单调函数,则可知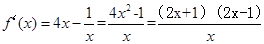 ,则可知函数的单调区间为k-1<0.5,k-1
,则可知函数的单调区间为k-1<0.5,k-1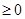 ,故可知k的取值范围是
,故可知k的取值范围是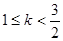 ,故答案为B.
,故答案为B.
考点:函数的单调性
点评:主要是考查了函数单调性的运用,属于基础题。

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
给出下列函数① ②
② ③
③ ④
④ ,其中是奇函数的是( )
,其中是奇函数的是( )
| A.①② | B.①④ | C.②④ | D.③④ |
已知 ,符号
,符号 表示不超过
表示不超过 的最大整数,若函数
的最大整数,若函数 有且仅有3个零点,则
有且仅有3个零点,则 的取值范围是( )
的取值范围是( )
A. |
B.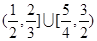 |
C. |
D. |
已知函数 是定义在区间
是定义在区间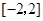 上的偶函数,当
上的偶函数,当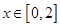 时,
时, 是减函数,如果不等式
是减函数,如果不等式 成立,求实数
成立,求实数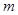 的取值范围.( )
的取值范围.( )
A.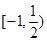 | B.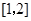 | C. | D.(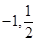 ) ) |
已知定义在 上的函数
上的函数 满足
满足 ,当
,当 时,
时, 单调递增,若
单调递增,若 且
且 ,则
,则 的值( )
的值( )
| A.可能为0 | B.恒大于0 | C.恒小于0 | D.可正可负 |
函数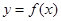 的图像如图所示,在区间
的图像如图所示,在区间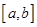 上可找到
上可找到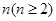 个不同的数
个不同的数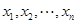 ,使得
,使得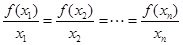 ,则
,则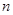 的取值范围为( )
的取值范围为( )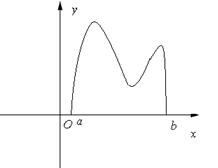
A.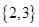 | B.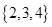 |
C.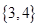 | D. |
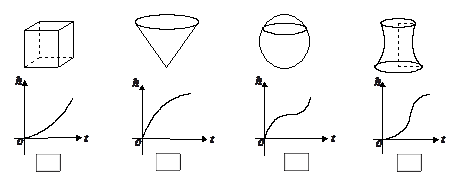
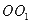 底面半径为1,高为
底面半径为1,高为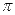 ,
,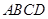 是圆柱的一个轴截面.动点
是圆柱的一个轴截面.动点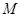 从点
从点 出发沿着圆柱的侧面到达点
出发沿着圆柱的侧面到达点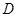 其距离最短时在侧面留下的曲线
其距离最短时在侧面留下的曲线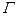 如图所示.现将轴截面
如图所示.现将轴截面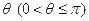 后,边
后,边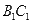 与曲线
与曲线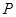 ,设
,设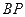 的长度为
的长度为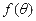 ,则
,则 的图象大致为( )
的图象大致为( )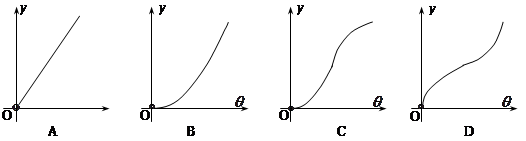
 ,如果存在区间
,如果存在区间 ,同时满足下列条件:
,同时满足下列条件: 在
在 存在“和谐区间”,则
存在“和谐区间”,则 的取值范围是( )
的取值范围是( )

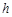 和时间
和时间 之间的关系,其中正确的有( )
之间的关系,其中正确的有( )