题目内容
对于函数 ,如果存在区间
,如果存在区间 ,同时满足下列条件:
,同时满足下列条件:
① 在
在 内是单调的;②当定义域是
内是单调的;②当定义域是 时,
时, 的值域也是
的值域也是 ,则称
,则称 是该函数的“和谐区间”.若函数
是该函数的“和谐区间”.若函数 存在“和谐区间”,则
存在“和谐区间”,则 的取值范围是( )
的取值范围是( )
A. | B.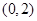 | C.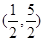 | D. |
A
解析试题分析:由题意可得函数 在区间
在区间 上是单调的,所以
上是单调的,所以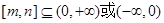 ,则
,则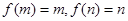 ,故m、n是方程
,故m、n是方程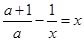 的两个同号的实数根,即方程
的两个同号的实数根,即方程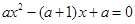 有两个同号的实数根,注意到
有两个同号的实数根,注意到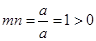 ,故只需
,故只需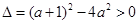 ,解得
,解得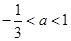 ,结合
,结合 ,可得
,可得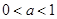 。故选A。
。故选A。
考点:函数的单调性
点评:本题考查函数单调性的判断和一元二次方程的根的分布,属基础题.

练习册系列答案
相关题目
函数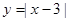 的单调递减区间为( )
的单调递减区间为( )
A.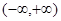 | B.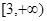 | C.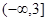 | D.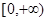 |
若函数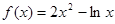 在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )
在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )
A. | B.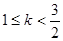 |
C.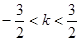 | D.不存在这样的实数k |
下列函数中,与函数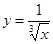 定义域相同的函数为
定义域相同的函数为
A.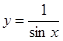 | B. | C.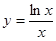 | D.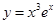 |
函数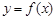 的图像如图所示,在区间
的图像如图所示,在区间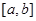 上可找到
上可找到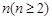 个不同的数
个不同的数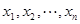 ,使得
,使得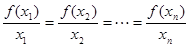 ,则
,则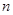 的取值范围为( )
的取值范围为( )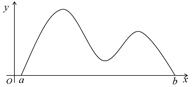
A.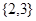 | B.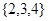 |
C.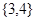 | D.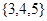 |
函数f(x)=2x2-mx+2当x∈[-2,+∞)时是增函数,则m的取值范围是( )
| A.(-∞,+∞) | B.[8,+∞) | C.(-∞,-8] | D.(-∞,8] |
 ,其中
,其中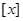 表示不超过实数
表示不超过实数 的最大整数.若关于
的最大整数.若关于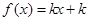 有三个不同的实根,则实数
有三个不同的实根,则实数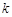 的取值范围是( )
的取值范围是( )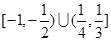
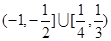
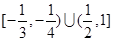
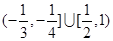
 的图象是( )
的图象是( )
 和
和 ,动点
,动点 在直线
在直线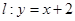 上移动,椭圆
上移动,椭圆 以
以 为焦点且经过点
为焦点且经过点 ,记椭圆
,记椭圆 ,则函数
,则函数 的大致图像( )
的大致图像( )