题目内容
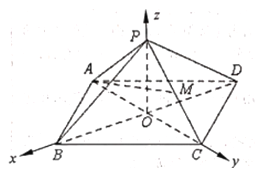
【题目】如图,在空间直角坐标系![]() 中,已知正四棱锥
中,已知正四棱锥![]() 的高
的高![]() ,点
,点![]() 和
和![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,且
轴上,且![]() ,点
,点![]() 是棱
是棱![]() 的中点.
的中点.
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出![]() 和平面PAB的法向量,利用向量法能求出直线AM与平面PAB所成角的正弦值.(2)求平面PBC的法向量和平面PAB的法向量,利用向量法求二面角A﹣PB﹣C的余弦值.
和平面PAB的法向量,利用向量法能求出直线AM与平面PAB所成角的正弦值.(2)求平面PBC的法向量和平面PAB的法向量,利用向量法求二面角A﹣PB﹣C的余弦值.
(1)P(0,0,2),A(0,-1,0),B(1,0,0),M(0,![]() ,1),
,1),
![]() =(0,1,2),
=(0,1,2),![]() =(1,1,0),设平面PAB的法向量为
=(1,1,0),设平面PAB的法向量为![]() =(x,y,z),
=(x,y,z),
则![]() ,取x=2,y=-2,z=1,
,取x=2,y=-2,z=1,![]() =(2,-2,1),
=(2,-2,1),
![]() =(0,
=(0,![]() ,1),
,1),
![]() ,得cosθ=
,得cosθ=![]() =
=![]() ,
,
即线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(2)C(0,1,0),P(0,0,2),B(1,0,0)
![]() =(-1,0,2),
=(-1,0,2),![]() =(-1,1,0),设平面PBC的法向量为
=(-1,1,0),设平面PBC的法向量为![]() =(x,y,z),
=(x,y,z),
则![]() ,取x=2,y=2,z=1,
,取x=2,y=2,z=1,![]() =(2,2,1),
=(2,2,1),
![]() ,得cosα=
,得cosα=![]() ,
,
二面角![]() 的余弦值为
的余弦值为![]() .
.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案【题目】某媒体对“男女延迟退休”这一公众关注的问题进行了民意调查,下表是在某单位调查后得到的数据(人数):
赞同 | 反对 | 合计 | |
男 | 5 | 6 | 11 |
女 | 11 | 3 | 14 |
合计 | 16 | 9 | 25 |
(1)能否有90%以上的把握认为对这一问题的看法与性别有关?
(2)进一步调查:
①从赞同“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行陈述发言,求事件“男士和女士各至少有
人进行陈述发言,求事件“男士和女士各至少有![]() 人发言”的概率;
人发言”的概率;
②从反对“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行座谈,设选出的
人进行座谈,设选出的![]() 人中女士人数为
人中女士人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
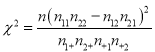
【题目】为提倡节能减排,同时减轻居民负担,广州市积极推进“一户一表”工程![]() 非一户一表用户电费采用“合表电价”收费标准:
非一户一表用户电费采用“合表电价”收费标准:![]() 元
元![]() 度
度![]() “一户一表”用户电费采用阶梯电价收取,其11月到次年4月起执行非夏季标准如下:
“一户一表”用户电费采用阶梯电价收取,其11月到次年4月起执行非夏季标准如下:
第一档 | 第二档 | 第三档 | |
每户每月用电量 |
|
|
|
电价 |
|
|
|
例如:某用户11月用电410度,采用合表电价收费标准,应交电费![]() 元,若采用阶梯电价收费标准,应交电费
元,若采用阶梯电价收费标准,应交电费![]() 元.
元.
为调查阶梯电价是否能到“减轻居民负担”的效果,随机调查了该市100户的11月用电量,工作人员已经将90户的月用电量填在下面的频率分布表中,最后10户的月用电量![]() 单位:度
单位:度![]() 为:88、268、370、140、440、420、520、320、230、380.
为:88、268、370、140、440、420、520、320、230、380.

(1)在答题卡中完成频率分布表,并绘制频率分布直方图;

![]() 根据已有信息,试估计全市住户11月的平均用电量
根据已有信息,试估计全市住户11月的平均用电量![]() 同一组数据用该区间的中点值作代表
同一组数据用该区间的中点值作代表![]() ;
;
![]() 设某用户11月用电量为x度
设某用户11月用电量为x度![]() ,按照合表电价收费标准应交
,按照合表电价收费标准应交![]() 元,按照阶梯电价收费标准应交
元,按照阶梯电价收费标准应交![]() 元,请用x表示
元,请用x表示![]() 和
和![]() ,并求当
,并求当![]() 时,x的最大值,同时根据频率分布直方图估计“阶梯电价”能否给不低于
时,x的最大值,同时根据频率分布直方图估计“阶梯电价”能否给不低于![]() 的用户带来实惠?
的用户带来实惠?
【题目】某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B,要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
产品A(件) | 产品B(件) | ||
研制成本与塔载 | 20 | 30 | 计划最大资 |
产品重量(千克/件) | 10 | 5 | 最大搭载 |
预计收益(万元/件) | 80 | 60 |
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?