题目内容
已知α,β是两个不同的平面,m,n是两条不同的直线,给出下列命题:
①若m⊥α,m⊥β,则α∥β;
②若m?α,n?α,m∥β,n∥β,则α∥β;
③如果m?α,n?α,m、n是异面直线,那么n与a相交;
④若α∩β=m,n∥m,且n?α,n?β,则n∥α且n∥β.
其中正确的命题是( )
①若m⊥α,m⊥β,则α∥β;
②若m?α,n?α,m∥β,n∥β,则α∥β;
③如果m?α,n?α,m、n是异面直线,那么n与a相交;
④若α∩β=m,n∥m,且n?α,n?β,则n∥α且n∥β.
其中正确的命题是( )
| A、①② | B、②③ | C、③④ | D、①④ |
分析:根据空间面面平行的判定方法,可判断①;根据面面平行的判定定理,可判断②;根据空间异面直线的几何特征,可判断③;根据线面平行的判定定理可判断④,进而得到答案.
解答:解:若m⊥α,m⊥β,则α∥β,故①正确;
若m?α,n?α,m∥β,n∥β,当m,n相交时,则α∥β,但m,n平行时,结论不一定成立,故②错误;
如果m?α,n?α,m、n是异面直线,那么n与a相交或平行,故③错误;
若α∩β=m,n∥m,n?α,则n∥α,同理由n?β,可得n∥β,故④正确;
故正确的命题为:①④
故选:D
若m?α,n?α,m∥β,n∥β,当m,n相交时,则α∥β,但m,n平行时,结论不一定成立,故②错误;
如果m?α,n?α,m、n是异面直线,那么n与a相交或平行,故③错误;
若α∩β=m,n∥m,n?α,则n∥α,同理由n?β,可得n∥β,故④正确;
故正确的命题为:①④
故选:D
点评:本题以命题的真假判断为载体,考查空间线面关系的判断,难度不大,属于基础题.

练习册系列答案
相关题目
 ,
, 是两个不重合的平面,给出下列4个命题:①若
是两个不重合的平面,给出下列4个命题:①若 ,
, ,
, ,则
,则 ;②若
;②若 ,
, ,则
,则 ,则
,则 ;④若
;④若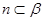 ,
, ,则
,则 ,其中真命题为( )
,其中真命题为( )