题目内容
7.已知函数f(x)=ax3+bx2+cx是R上的奇函数,且f(1)=3,f(2)=12.(1)求a,b,c的值;
(2)设g(x)=(m+1)lnx+m$\frac{f(x)}{x}$+1-2m,讨论g(x)的单调性
(3)当m≤-2时,解不等式g(x)≤m+5-4x.
分析 (1)根据函数的奇偶性性和条件,建立方程即可求a,b,c的值;
(2)由(1)得g(x)=(m+1)lnx+mx2+1,则g′(x)=$\frac{2{mx}^{2}+m+1}{x}$,①当m≥0时,g′(x)>0恒成立,②当m≤-1时,g′(x)≤0恒成立,(仅当a=-1时取等号)③当-1<m<0时,0<x<$\sqrt{\frac{-m-1}{2m}}$时,g′(x)>0;x>$\sqrt{\frac{-m-1}{2m}}$时,g′(x)<0,进而可得g(x)的单调性
(3)不等式g(x)≤m+5-4x可化为(m+1)lnx+mx2+4x-m-4≤0,令h(x)=(m+1)lnx+mx2+4x-m-4,利用导数法可得:函数为减函数,且h(1)=0,进而可得不等式的解集.
解答 解:(1)∵函数f(x)=ax3+bx2+cx是R上的奇函数,
∴f(-x)=-f(x),
∴b=0,
∵f(1)=3,f(2)=12.
∴$\left\{\begin{array}{l}a+c=3\\ 8a+2c=12\end{array}\right.$,
解得 $\left\{\begin{array}{l}a=1\\ c=2\end{array}\right.$,
∴a,b,c的值分别为1,0,2;
(2)由(1)得f(x)=x3+2x,
∴g(x)=(m+1)lnx+m$\frac{f(x)}{x}$+1-2m=(m+1)lnx+mx2+1,
则g′(x)=$\frac{2{mx}^{2}+m+1}{x}$,
①当m≥0时,g′(x)>0恒成立,
∴g(x)在区间(0,+∞)上为增函数;
②当m≤-1时,g′(x)≤0恒成立,(仅当a=-1时取等号)
∴g(x)在区间(0,+∞)上为减函数;
③当-1<m<0时,令g′(x)=0得x=$\sqrt{\frac{-m-1}{2m}}$,
易知0<x<$\sqrt{\frac{-m-1}{2m}}$时,g′(x)>0;x>$\sqrt{\frac{-m-1}{2m}}$时,g′(x)<0
∴g(x)增于(0,$\sqrt{\frac{-m-1}{2m}}$);减于($\sqrt{\frac{-m-1}{2m}}$,+∞)
综上所述,m≥0时,g(x)在区间(0,+∞)上为增函数;
m≤-1时,g(x)在区间(0,+∞)上为减函数
-1<m<0时,g(x)在区间(0,$\sqrt{\frac{-m-1}{2m}}$)上为增函数;在区间($\sqrt{\frac{-m-1}{2m}}$,+∞) 上为减函数…(8分)
(3)不等式g(x)≤m+5-4x可化为:(m+1)lnx+mx2+1≤m+5-4x,即(m+1)lnx+mx2+4x-m-4≤0,
令h(x)=(m+1)lnx+mx2+4x-m-4,
则h′(x)=$\frac{2{mx}^{2}+4x+m+1}{x}$=$\frac{1}{x}[2m(x+\frac{1}{m})^{2}+\frac{(m+2)(m-1)}{m}]$,
当m≤-2时,h′(x)<0恒成立,
故h(x)在区间(0,+∞)上为减函数;
由h(1)=0得:h(x)≤0?x≥1,
即不等式g(x)≤m+5-4x的解集为[1,+∞).
点评 本题考查的知识点是函数奇偶性的性质,函数单调性的判断与证明,函数的最值,是函数图象与性质和导数的综合应用,难度中档.

| A. | (-$\frac{π}{12}$,0) | B. | ($\frac{π}{12}$,0) | C. | (-$\frac{π}{6}$,0) | D. | ($\frac{π}{6}$,0) |
| A. | {-1,-2,-3,1} | B. | {-1,0,1} | C. | {-1,-3} | D. | {-2,-3} |
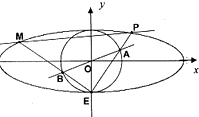 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆C2:x2+y2=b2,已知椭圆C1过点(1,$\frac{\sqrt{2}}{2}$),焦距为2.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆C2:x2+y2=b2,已知椭圆C1过点(1,$\frac{\sqrt{2}}{2}$),焦距为2.