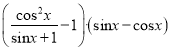Question

【题目】对于两个图形F1 ， F2 ， 我们将图象F1上任意一点与图形F2上的任意一点间的距离中的最小值，叫作图形F1与F2图形的距离，若两个函数图象的距离小于1，则这两个函数互为“可及函数”，给出下列几对函数，其中互为“可及函数”的是 ． （写出所有正确命题的编号） ①f（x）=cosx，g（x）=2；
②f（x）=ex ． g（x）=x；
③f（x）=log2（x2﹣2x+5），g（x）=sin ﹣x；
④f（x）=x+ ，g（x）=lnx+2．

Answer 1

【答案】②④
【解析】解：①f（x）=cosx的最低点与g（x）=2的距离等于1，故不满足题意； ②f（x）=ex ， 则f′（x）=ex ， 设切点为（a，ea），则ea=1，∴a=0，∴切点为（（0，1），切线方程为y=x+1，则与g（x）=x的距离为 ＜1，满足题意；
③f（x）=log2（x2﹣2x+5）≥2，g（x）=sin x﹣ ＜0，∴两个函数图象的距离大于等于1，不满足题意；
④x= 时，f（x）=x+ =2 ，g（x）=lnx+2=ln +2，两个函数图象的距离小于1，满足题意；
所以答案是：②④