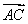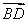ΧβΡΩΡΎ»ί
Ε‘”ΎΕ®“ε‘ΎR…œΒΡΚ· ΐf(x)”–“‘œ¬ΈεΗωΟϋΧβΘΚ
ΔΌ»τyΘΫf(x) «ΤφΚ· ΐΘ§‘ρyΘΫf(xΘ≠1)ΒΡΆΦœσΙΊ”ΎA(1,0)Ε‘≥ΤΘΜ
ΔΎ»τΕ‘”Ύ»Έ“βxΓ RΘ§”–f(xΘ≠1)ΘΫf(xΘΪ1)Θ§‘ρf(x)ΙΊ”Ύ÷±œΏxΘΫ1Ε‘≥ΤΘΜ
ΔέΚ· ΐyΘΫf(xΘΪ1)”κyΘΫf(1Θ≠x)ΒΡΆΦœσΙΊ”Ύ÷±œΏxΘΫ1Ε‘≥ΤΘΜ
Δή»γΙϊΚ· ΐyΘΫf(x)¬ζΉψf(xΘΪ1)ΘΫf(1Θ≠x)Θ§f(xΘΪ3)ΘΫf(3Θ≠x)Θ§Ρ«Ο¥ΗΟΚ· ΐ“‘4ΈΣ÷ήΤΎΘ°
Τδ÷–’ΐ»ΖΟϋΧβΒΡ–ρΚ≈ΈΣ________Θ°
ΔΌΔή
ΓΨΫβΈωΓΩΔΌΤφΚ· ΐΆΦœσ”““Τ“ΜΗωΒΞΈΜΘ§Ε‘≥Τ÷––Ρ±δΈΣ(1,0)ΘΜΔΎ»τΕ‘”Ύ»Έ“βxΓ RΘ§”–f(xΘ≠1)ΘΫf(xΘΪ1)Θ§‘ρf(x)ΘΫf(xΘΪ2)ΘΜΔέΝΫΚ· ΐΆΦœσΙΊ”Ύ÷±œΏxΘΫ0Ε‘≥ΤΘΜΔήf(xΘΪ1)ΘΫf(1Θ≠x)ΘΫf[(Θ≠2Θ≠x)ΘΪ3]ΘΫf[3Θ≠(Θ≠2Θ≠x)]ΘΫf(5ΘΪx)Θ§Γύf(x)ΘΫf(xΘΪ4)Θ§ΗΟΚ· ΐ“‘4ΈΣ÷ήΤΎΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ