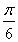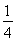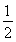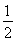已知等比数列{an}的所有项均为正数.首项a1＝1.且a4.3a3.a5成等差数列．(1)求数列{an}的通项公式,(2)数列{an+1-λan}的前n项和为Sn.若Sn＝2n-1(n∈N*).求实数λ的值．题目和参考答案——青夏教育精英家教网—

题目内容

已知等比数列{an}的所有项均为正数，首项a1＝1，且a4，3a3，a5成等差数列．

(1)求数列{an}的通项公式；

(2)数列{an＋1－λan}的前n项和为Sn，若Sn＝2n－1(n∈N*)，求实数λ的值．

（1）an＝2n－1.（2）λ＝1

【解析】(1)设数列{an}的公比为q，则由条件得q3，3q2，q4成等差数列，所以6q2＝q3＋q4，q≠0，此方程即q2＋q－6＝0，解得q＝－3(舍去)或q＝2，所以数列{an}的通项公式是an＝2n－1.

(2)an＋1－λan＝2n－λ·2n－1＝(2－λ)·2n－1，显然λ＝2不合题意，λ≠2时，数列{an＋1－λan}的前n项和为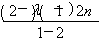＝(2－λ)·(2n－1)，与已知比较可得λ＝1.

练习册系列答案

相关题目

已知a∈R，函数f(x)＝4x3－2ax＋a.

(1)求f(x)的单调区间；

(2)证明：当0≤x≤1时，f(x)＋|2－a|＞0.

对于定义在R上的函数f(x)有以下五个命题：

①若y＝f(x)是奇函数，则y＝f(x－1)的图象关于A(1,0)对称；

②若对于任意x∈R，有f(x－1)＝f(x＋1)，则f(x)关于直线x＝1对称；

③函数y＝f(x＋1)与y＝f(1－x)的图象关于直线x＝1对称；

④如果函数y＝f(x)满足f(x＋1)＝f(1－x)，f(x＋3)＝f(3－x)，那么该函数以4为周期．

其中正确命题的序号为________．

下列命题中正确的是(　　)

A．若命题p为真命题，命题q为假命题，则命题“p∧q”为真命题

B．“sinα＝”是“α＝的充分不必要条件”

C．l为直线，α，β为两个不同的平面，若l⊥β，α⊥β，则l∥α

D．命题“?x∈R,2x＞0”的否定是“?x0∈R,2x0≤0”

已知a∈R，则“a＞2”是“a2＞2a”成立的(　　)

A．充分不必要条件 B．必要不充分条件

C．充要条件 D．既不充分也不必要条件

已知函数f(x)是R上的单调递增函数且为奇函数，数列{an}是等差数列，a3>0，则f(a1)＋f(a3)＋f(a5)的值(　　)

A．恒为正数

B．恒为负数

C．恒为0

D．可以为正数也可以为负数

公比为2的等比数列{an}的各项都是正数，且a4a10＝16，则a6＝(　　)

A．1 B．2 C．4 D．8

已知向量p＝(an，2n)，q＝(2n＋1，－an＋1)，n∈N*，p与q垂直，且a1＝1.

(1)求数列{an}的通项公式；

(2)若数列{bn}满足bn＝log2an＋1，求数列{an·bn}的前n项和Sn.

函数f(x)＝1－xlog2x的零点所在的区间是(　　)

A.， B.，1 C．(1，2) D．(2，3)

试题分类