题目内容
椭圆
 与圆
与圆 (
( 为椭圆半焦距)有四个不同交点,则离心率的取值范围是 ( )
为椭圆半焦距)有四个不同交点,则离心率的取值范围是 ( )
A. | B. | C. | D. |
A
解析试题分析:∵椭圆椭圆
 与圆
与圆 的中心都在原点,
的中心都在原点,
且它们有四个交点,
∴圆的半径满足 ,
,
由 ,得2c>b,再平方,4c2>b2,
,得2c>b,再平方,4c2>b2,
在椭圆中,a2=b2+c2<5c2,
∴e= >
> ;
;
由 ,得b+2c<2a,
,得b+2c<2a,
再平方,b2+4c2+4bc<4a2,
∴3c2+4bc<3a2,
∴4bc<3b2,
∴4c<3b,
∴16c2<9b2,
∴16c2<9a2-9c2,
∴9a2>25c2,
∴ ,
,
∴e< .
.
综上所述, .
.
故选A.
考点:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,圆的简单性质等基础知识.
点评:典型题,本题在考查数学知识的同时,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想。

练习册系列答案
相关题目
已知双曲线 的右焦点是F, 过点F且倾角为600的直线与双曲线的右支有且只有一个交点,则此双曲线的离心率的范围是( )
的右焦点是F, 过点F且倾角为600的直线与双曲线的右支有且只有一个交点,则此双曲线的离心率的范围是( )
A. | B.(1,2) | C. | D. |
要使直线 与焦点在
与焦点在 轴上的椭圆
轴上的椭圆 总有公共点,实数
总有公共点,实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
方程 所表示的曲线是( )
所表示的曲线是( )
| A.双曲线 | B.椭圆 | C.双曲线的一部分 | D.椭圆的一部分 |
双曲线 的一条渐近线的倾斜角为
的一条渐近线的倾斜角为 ,离心率为
,离心率为 ,则
,则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
双曲线 的渐近线与圆
的渐近线与圆 相切,则
相切,则 = ( )
= ( )
A. | B.2 | C.3 | D.6 |
设 是椭圆E:
是椭圆E: 的左右焦点,P在直线
的左右焦点,P在直线 上一点,
上一点, 是底角为
是底角为 的等腰三角形,则椭圆E的离心率为( )
的等腰三角形,则椭圆E的离心率为( )
A. | B. | C. | D. |
 的左焦点
的左焦点 ,作圆
,作圆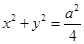 的切线,切点为E,延长FE交曲线右支于点P,若
的切线,切点为E,延长FE交曲线右支于点P,若 ,则双曲线的离心率为( )
,则双曲线的离心率为( )



 (a>
(a> )中,记左焦点为F,右顶点为A,短轴上方的端点为B,若角
)中,记左焦点为F,右顶点为A,短轴上方的端点为B,若角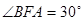 ,则椭圆的离心率为( )
,则椭圆的离心率为( )


