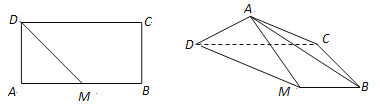
题目内容
【题目】设椭圆![]() 的离心率是
的离心率是![]() ,A、B分别为椭圆的左顶点、上顶点,原点O到AB所在直线的距离为
,A、B分别为椭圆的左顶点、上顶点,原点O到AB所在直线的距离为![]() .
.
(I)求椭圆C的方程;
(Ⅱ)已知直线![]() 与椭圆相交于不同的两点M,N(均不是长轴的端点),
与椭圆相交于不同的两点M,N(均不是长轴的端点),![]() ,垂足为H,且
,垂足为H,且![]() ,求证:直线
,求证:直线![]() 恒过定点.
恒过定点.
【答案】(I)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
(I)直线AB的方程为:![]() 1,化为:bx﹣ay+ab=0.原点O到AB所在直线的距离为
1,化为:bx﹣ay+ab=0.原点O到AB所在直线的距离为![]() ,可得
,可得![]() ,化为:12(a2+b2)=7a2b2,又
,化为:12(a2+b2)=7a2b2,又![]() ,
,
a2=b2+c2.联立解出即可得出.
(Ⅱ)设M(x1,y1),N(x2,y2).联立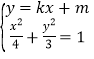 ,化为:(3+4k2)x2+8kmx+4m2﹣12=0,△>0,由AH⊥MN,垂足为H,且
,化为:(3+4k2)x2+8kmx+4m2﹣12=0,△>0,由AH⊥MN,垂足为H,且![]() 2
2![]()
![]() ,可得AM⊥AN.可得
,可得AM⊥AN.可得![]() (x1+2)(x2+2)+y1y2=(2+km)(x1+x2)+(1+k2)x1x2+4+m2=0,把根与系数的关系代入化简即可得出.
(x1+2)(x2+2)+y1y2=(2+km)(x1+x2)+(1+k2)x1x2+4+m2=0,把根与系数的关系代入化简即可得出.
(I)直线AB的方程为:![]() 1,化为:bx﹣ay+ab=0.
1,化为:bx﹣ay+ab=0.
∵原点O到AB所在直线的距离为![]() ,∴
,∴![]() ,
,
化为:12(a2+b2)=7a2b2,又![]() ,a2=b2+c2.
,a2=b2+c2.
联立解得a=2,b![]() ,c=1.
,c=1.
∴椭圆C的方程为:![]() 1.
1.
(Ⅱ)设M(x1,y1),N(x2,y2).
联立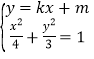 ,化为:(3+4k2)x2+8kmx+4m2﹣12=0,
,化为:(3+4k2)x2+8kmx+4m2﹣12=0,
△=64k2m2﹣4(3+4k2)(4m2﹣12)>0,(*)
∴x1+x2![]() ,x1x2
,x1x2![]() ,
,
∵AH⊥MN,垂足为H,且![]() 2
2![]()
![]() ,
,
∴AM⊥AN.
∴![]() (x1+2)(x2+2)+y1y2=(x1+2)(x2+2)+(kx1+m)(kx2+m)=(2+km)(x1+x2)+(1+k2)x1x2+4+m2=0,
(x1+2)(x2+2)+y1y2=(x1+2)(x2+2)+(kx1+m)(kx2+m)=(2+km)(x1+x2)+(1+k2)x1x2+4+m2=0,
∴﹣(2+km)![]() (1+k2)
(1+k2)![]() 4+m2,
4+m2,
∴4k2﹣16km+7m2=0,
解得k![]() m,或
m,或![]() m.满足(*)
m.满足(*)
∴直线l方程为:y=m(![]() x+1),或y=m
x+1),或y=m![]() .
.
直线y=m(![]() x+1)恒过定点A(﹣2,0),舍去.
x+1)恒过定点A(﹣2,0),舍去.
直线y=m![]() 恒过定点(
恒过定点(![]() ,0),
,0),
∴直线l恒过定点(![]() ,0).
,0).

 阅读快车系列答案
阅读快车系列答案【题目】现行的个税法修正案规定:个税免征额由原来的2000元提高到3500元,并给出了新的个人所得税税率表:
全月应纳税所得额 | 税率 |
不超过1500元的部分 | 3% |
超过1500元至4500元的部分 | 10% |
超过4500元至9000元的部分 | 20% |
超过9000元至35000元的部分 | 25% |
…… | … |
例如某人的月工资收入为5000元,那么他应纳个人所得税为:![]() (元).
(元).
(Ⅰ)若甲的月工资收入为6000元,求甲应纳的个人收的税;
(Ⅱ)设乙的月工资收入为![]() 元,应纳个人所得税为
元,应纳个人所得税为![]() 元,求
元,求![]() 关于
关于![]() 的函数;
的函数;
(Ⅲ)若丙某月应纳的个人所得税为1000元,给出丙的月工资收入.(结论不要求证明)
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号,某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
试销单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)已知变量x,y具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程![]() ;
;
(2)用![]() 表示用(1)中所求的线性回归方程得到的与
表示用(1)中所求的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数
称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(参考公式: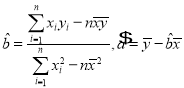 ;参考数据:
;参考数据:![]() )
)