题目内容
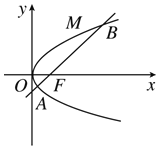
【题目】如图所示，斜率为1的直线过抛物线
的焦点F，与抛物线交于A，B两点且
，M为抛物线弧AB上的动点．
求抛物线的方程；
求
的最大值．
【答案】（1）；（2）
.
【解析】
设直线
方程为
，与
联立，得
，由韦达定理结合抛物线的定义可得
，可得
的值，从而可得结果；
设与直线平行且与抛物线相切的直线方程为
，代入抛物线方程，得
，利用判别式为零可求得
的值，计算可得两直线间的距离，由三角形面积公式计算即可得答案．
由条件知
：，
与联立，消去y，得，
则
由抛物线定义得
．
又因为
，即
，
则抛物线的方程为
；
由知，且：
，
设与直线AB平行且与抛物线相切的直线方程为，
代入抛物线方程，得．
由
，得
．
与直线AB平行且与抛物线相切的直线方程为
两直线间的距离为
，
故
的最大值为
．
练习册系列答案
相关题目
