题目内容
某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含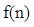 个小正方形.
个小正方形.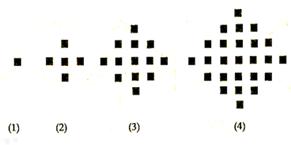
(Ⅰ)求出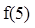 ;
;
(Ⅱ)利用合情推理的“归纳推理思想”归纳出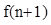 与
与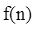 的关系式,
的关系式,
(Ⅲ)根据你得到的关系式求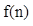 的表达式.
的表达式.
(Ⅰ)41(Ⅱ)f(n+1)-f(n)=4n(Ⅲ)f(n)=2n2-2n+1
解析试题分析:(Ⅰ)先分别观察给出正方体的个数为:1,1+4,1+4+8, 从而得出f(5);
(Ⅱ)将(Ⅰ)总结一般性的规律:f(n+1)与f(n)的关系式,
(Ⅲ)再从总结出来的一般性的规律转化为特殊的数列再求解即得.
试题解析:(Ⅰ) f(1)=1,f(2)=5,f(3)=13,f(4)=25, 2分
f(1)=1,f(2)=5,f(3)=13,f(4)=25, 2分 f(5)=25+4×4=41. 4分
f(5)=25+4×4=41. 4分
(Ⅱ) f(2)-f(1)=4=4×1. f(3)-f(2)=8=4×2,
f(2)-f(1)=4=4×1. f(3)-f(2)=8=4×2,
f(4)-f(3)=12=4×3, f(5)-f(4)=16=4×4, 6分
由上式规律得出f(n+1)-f(n)=4n. 8分
(Ⅲ) f(2)-f(1)=4×1, f(3)-f(2)=4×2, f(4)-f(3)=4×3, f(n-1)-f(n-2)=4·(n-2), f(n)-f(n-1)=4·(n-1) 10分
f(2)-f(1)=4×1, f(3)-f(2)=4×2, f(4)-f(3)=4×3, f(n-1)-f(n-2)=4·(n-2), f(n)-f(n-1)=4·(n-1) 10分 f(n)-f(1)="4[1+2+" +(n-2)+(n-1)]=2(n-1)·n,
f(n)-f(1)="4[1+2+" +(n-2)+(n-1)]=2(n-1)·n, f(n)=2n2-2n+1 12分
f(n)=2n2-2n+1 12分
考点:归纳推理;进行简单的合情推理.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
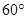 ;
;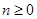 ,试用分析法证明:
,试用分析法证明: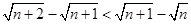 .
.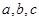 为三角形
为三角形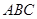 的三边,求证:
的三边,求证: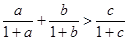

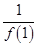 +
+ +
+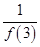 +…+
+…+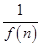 <
<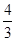 .
. ,
,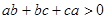 ,
,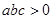 ,求证:
,求证: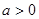 ,
,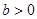 ,
,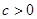 .
. .
.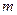 的
的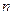 次方幂有如下分解方
次方幂有如下分解方 式:
式: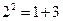 ;
;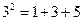 ;
; 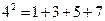 ;
;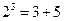 ;
; ;
;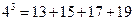 .
.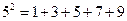 ,
,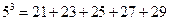 .
.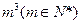 的分解中最大的加数是419,
的分解中最大的加数是419, .
.