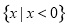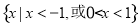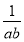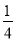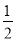题目内容
已知函数f(x)=x- ,g(x)=x2-2ax+4,若任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),则实数a的取值范围是______.
,g(x)=x2-2ax+4,若任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),则实数a的取值范围是______.
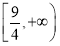
【解析】由于f′(x)=1+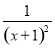 >0,因此函数f(x)在[0,1]上单调递增,所以x∈[0,1]时,f(x)min=f(0)=-1.根据题意可知存在x∈[1,2],使得g(x)=x2-2ax+4≤-1,即x2-2ax+5≤0,即a≥
>0,因此函数f(x)在[0,1]上单调递增,所以x∈[0,1]时,f(x)min=f(0)=-1.根据题意可知存在x∈[1,2],使得g(x)=x2-2ax+4≤-1,即x2-2ax+5≤0,即a≥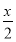 +
+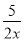 能成立,令h(x)=
能成立,令h(x)=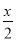 +
+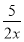 ,则要使a≥h(x)在x∈[1,2]能成立,只需使a≥h(x)min,又函数h(x)=
,则要使a≥h(x)在x∈[1,2]能成立,只需使a≥h(x)min,又函数h(x)=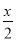 +
+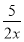 在x∈[1,2]上单调递减(可利用导数判断),所以h(x)min=h(2)=
在x∈[1,2]上单调递减(可利用导数判断),所以h(x)min=h(2)=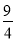 ,故只需a≥
,故只需a≥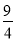 .
.

练习册系列答案
相关题目