题目内容
(12分)已知各项均为正数的数列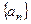 前
前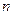 项和为
项和为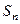 ,首项为
,首项为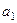 ,且
,且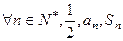 成等差数列.
成等差数列.
(1)求数列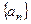 的通项公式;
的通项公式;
(2)若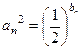 ,设
,设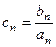 ,求数列
,求数列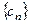 的前
的前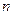 项和
项和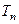 .
.
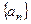 前
前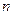 项和为
项和为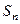 ,首项为
,首项为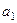 ,且
,且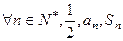 成等差数列.
成等差数列.(1)求数列
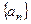 的通项公式;
的通项公式;(2)若
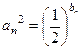 ,设
,设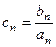 ,求数列
,求数列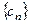 的前
的前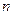 项和
项和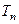 .
.(1)an=a1·2n-1=
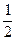 ×2n-1=2n-2
×2n-1=2n-2(2)Tn=
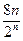
解(1)由题意知2an=Sn+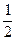 ,an>0
,an>0
当n=1时,2a1=a1+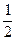 ∴a1=
∴a1=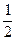
当n≥2时,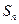 =2an-
=2an-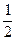 ,Sn-1=2an-1-
,Sn-1=2an-1-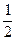
两式相减得an=2an-2an-1
整理得: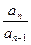 =2 ………………………………………………………4分
=2 ………………………………………………………4分
∴数列{an}是以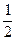 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.
an=a1·2n-1=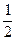 ×2n-1=2n-2 ………………………………………………5分
×2n-1=2n-2 ………………………………………………5分
(2)an2=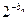 =22n-4 ∴bn=4-2n …………………6分
=22n-4 ∴bn=4-2n …………………6分
Cn=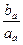 =
=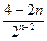 =
=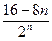
Tn=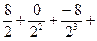 …
…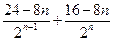 ①
①
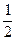 Tn=
Tn=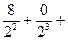 …+
…+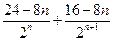 ②
②
①—②得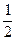 Tn=4-8
Tn=4-8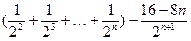 ……………………9分
……………………9分
=4-8·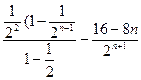 =4-4
=4-4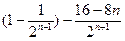
=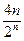 ……………11分
……………11分
∴Tn=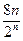 …………………………………………………………12分
…………………………………………………………12分
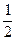 ,an>0
,an>0当n=1时,2a1=a1+
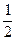 ∴a1=
∴a1=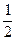
当n≥2时,
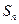 =2an-
=2an-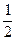 ,Sn-1=2an-1-
,Sn-1=2an-1-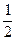
两式相减得an=2an-2an-1
整理得:
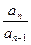 =2 ………………………………………………………4分
=2 ………………………………………………………4分∴数列{an}是以
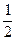 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.an=a1·2n-1=
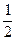 ×2n-1=2n-2 ………………………………………………5分
×2n-1=2n-2 ………………………………………………5分(2)an2=
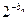 =22n-4 ∴bn=4-2n …………………6分
=22n-4 ∴bn=4-2n …………………6分Cn=
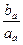 =
=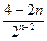 =
=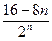
Tn=
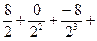 …
…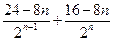 ①
①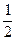 Tn=
Tn=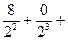 …+
…+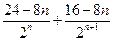 ②
②①—②得
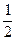 Tn=4-8
Tn=4-8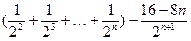 ……………………9分
……………………9分=4-8·
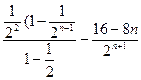 =4-4
=4-4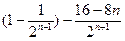
=
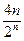 ……………11分
……………11分∴Tn=
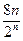 …………………………………………………………12分
…………………………………………………………12分
练习册系列答案
相关题目
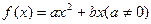 的导函数
的导函数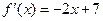 ,数列
,数列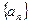 的前
的前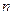 项和为
项和为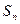 ,点
,点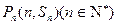 均在函数
均在函数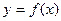 的图象上.
的图象上.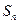 的最大值;
的最大值;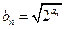 ,其中
,其中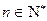 ,求
,求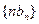 的前
的前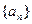 中,若
中,若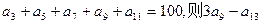 的值为( )
的值为( )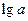
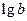
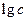
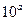
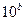
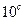
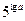
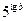
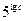
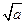
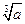
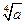
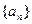 的前
的前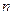 项和为
项和为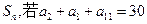 ,那么
,那么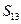 值的是 ( )
值的是 ( )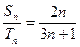 ,则
,则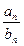 等于( )
等于( )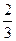
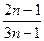
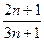
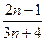
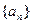 满足
满足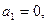
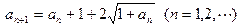 ,则
,则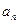 =___ .
=___ .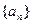 是公差为d的等差数列,其前n项和为Sn,则有
是公差为d的等差数列,其前n项和为Sn,则有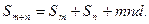 类似的,对于公比为q的等比数列
类似的,对于公比为q的等比数列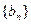 来说,设其前n项积为Tn,则关于
来说,设其前n项积为Tn,则关于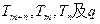 的一个关系式为 。
的一个关系式为 。