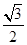题目内容
如图,设点P从原点沿曲线y=x2向点A(2,4)移动,记直线OP、曲线y=x2及直线x=2所围成的面积分别记为S1,S2,若S1=S2,则点P的坐标为 .


( ,
,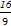 )
)
 ,
,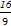 )
)【思路点拨】设直线OP的方程为y=kx,P点的坐标为(x0,y0),由S1=S2求出k的值,再求点P的坐标.
解:设直线OP的方程为y=kx,P点的坐标为(x0,y0),则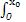 (kx-x2)dx=
(kx-x2)dx=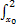 (x2-kx)dx,
(x2-kx)dx,
即( kx2-
kx2- x3)
x3)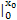 =(
=( x3-
x3- kx2)
kx2)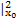 ,
,
即 k
k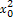 -
-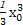 =
= -2k-(
-2k-(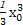 -
- k
k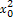 ),
),
解得k= ,即直线OP的方程为y=
,即直线OP的方程为y= x,所以点P的坐标为(
x,所以点P的坐标为( ,
,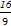 ).
).
解:设直线OP的方程为y=kx,P点的坐标为(x0,y0),则
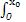 (kx-x2)dx=
(kx-x2)dx=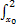 (x2-kx)dx,
(x2-kx)dx,即(
 kx2-
kx2- x3)
x3)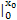 =(
=( x3-
x3- kx2)
kx2)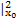 ,
,即
 k
k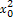 -
-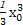 =
= -2k-(
-2k-(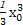 -
- k
k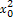 ),
),解得k=
 ,即直线OP的方程为y=
,即直线OP的方程为y= x,所以点P的坐标为(
x,所以点P的坐标为( ,
,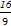 ).
).
练习册系列答案
相关题目
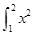 dx,S2=
dx,S2=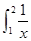 dx,S3=
dx,S3=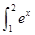 dx,则S1,S2,S3的大小关系为( )
dx,则S1,S2,S3的大小关系为( ) ,
, 围成的阴影部分的面积为( )
围成的阴影部分的面积为( )







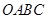 区域内任取一个点
区域内任取一个点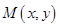 ,则点
,则点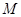 取自阴影部分的概率为( )
取自阴影部分的概率为( )




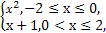 则
则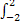 f(x)dx的值为( )
f(x)dx的值为( )
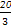
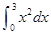 =_________.
=_________.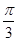 ,x=
,x=