Question

【题目】已知复数，，，，，满足，．

（1）若所对应点在圆上，求所对应点的轨迹；

（2）是否存在这样的直线，对应点在上，所对应点也在直线上？若存在，求出所有这些直线；若不存在，请说明理由．

Answer 1

【答案】（1）所对应点的轨迹是以为圆心，4为半径的圆；（2）存在且有两条或．

【解析】

（1）先根据，，得到，进而求得，然后将，，代入，利用复数相等，得到，，再代入求解.

（2）设存在且为．由，得到，．根据对应点在上，代入，利用待定系数法求解.

（1）因为，，所以，所以．

由，得．

所以 ．

∴，．

∵，

∴．

化简，得，

即．

所以所对应点的轨迹是以为圆心，4为半径的圆；

（2）由，得，．

假设满足条件的直线存在，则斜率存在，设为．

因为对应点在上，得，即．

∴．

所以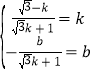．解方程组，得，，

所以这样的直线存在且有两条或．