题目内容
已知双曲线C的中心在坐标原点O,对称轴为坐标轴,点(-2,0)是它的一个焦点,并且离心率为 .
.(Ⅰ)求双曲线C的方程;
(Ⅱ)已知点M(0,1),设P(x,y)是双曲线C上的点,Q是点P关于原点的对称点,求
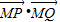 的取值范围.
的取值范围.
【答案】分析:(I)设双曲线方程为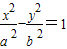 (a>0,b>0),依据题意,求出a、c、b的值,最后写出双曲线的标准方程和渐近线方程.
(a>0,b>0),依据题意,求出a、c、b的值,最后写出双曲线的标准方程和渐近线方程.
(Ⅱ)依题意有:Q(-x,-y),根据向量的坐标运算写出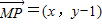 ,
,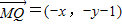 从而
从而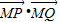 =-x2-y2+1再结合双曲线的范围得出x2≥3,从而求得
=-x2-y2+1再结合双曲线的范围得出x2≥3,从而求得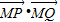 的取值范围.
的取值范围.
解答:解:(Ⅰ)设双曲线方程为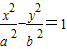 (a>0,b>0),半焦距c,
(a>0,b>0),半焦距c,
依题意得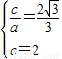 解得a=
解得a=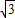 ,b=1,
,b=1,
∴所求双曲线C的方程为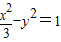 .
.
(Ⅱ)依题意有:Q(-x,-y),∴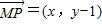 ,
,
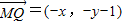
∴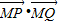 =-x2-y2+1
=-x2-y2+1
,又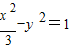 ,
,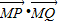 =
= ,由
,由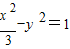 可得,x2≥3,
可得,x2≥3,
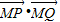 =
=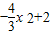 ≤-2故
≤-2故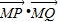 的取值范围x≤-2.
的取值范围x≤-2.
点评:本题考查双曲线的标准方程,以及双曲线的简单性质的应用.解答的关键是对双曲线标准方程的理解和向量运算的应用.
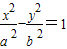 (a>0,b>0),依据题意,求出a、c、b的值,最后写出双曲线的标准方程和渐近线方程.
(a>0,b>0),依据题意,求出a、c、b的值,最后写出双曲线的标准方程和渐近线方程.(Ⅱ)依题意有:Q(-x,-y),根据向量的坐标运算写出
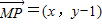 ,
,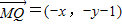 从而
从而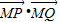 =-x2-y2+1再结合双曲线的范围得出x2≥3,从而求得
=-x2-y2+1再结合双曲线的范围得出x2≥3,从而求得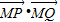 的取值范围.
的取值范围.解答:解:(Ⅰ)设双曲线方程为
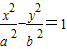 (a>0,b>0),半焦距c,
(a>0,b>0),半焦距c,依题意得
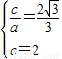 解得a=
解得a=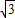 ,b=1,
,b=1,∴所求双曲线C的方程为
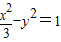 .
.(Ⅱ)依题意有:Q(-x,-y),∴
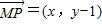 ,
,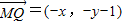
∴
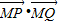 =-x2-y2+1
=-x2-y2+1,又
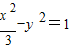 ,
,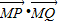 =
= ,由
,由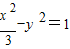 可得,x2≥3,
可得,x2≥3,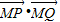 =
=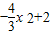 ≤-2故
≤-2故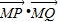 的取值范围x≤-2.
的取值范围x≤-2.点评:本题考查双曲线的标准方程,以及双曲线的简单性质的应用.解答的关键是对双曲线标准方程的理解和向量运算的应用.

练习册系列答案
相关题目