题目内容
(理) 在平面直角坐标系中,已知双曲线C的中心在原点,它的一个焦点坐标为(
,0),
=(2,1)、
=(2,-1)分别是两条渐近线的方向向量.任取双曲线C上的点P,其中
=m
+n
(m,n∈R),则m,n满足的一个等式是
| 5 |
| e1 |
| e2 |
| op |
| e1 |
| e2 |
4mn=1
4mn=1
.分析:根据
=(2,1)、
=(2,-1)是渐进线方向向量,进而可知双曲线渐近线方程,根据一个焦点坐标(
,0),进而求得a和b,求得双曲线方程,进而根据
=m
+n
,P在双曲线上,化简即可.
| e1 |
| e2 |
| 5 |
| op |
| e1 |
| e2 |
解答:解:因为c=
,所以
=(2,1)、
=(2,-1)是渐进线方向向量,
所以双曲线渐近线方程为y=±
x,
又c=
,a=2,b=1双曲线方程为
-
=1,
=m
+n
=(2m+2n,m-n),
点P是双曲线C上的点,
所以
-(m-n)2=1,化简得4mn=1.
故答案为:4mn=1.
| 5 |
| e1 |
| e2 |
所以双曲线渐近线方程为y=±
| 1 |
| 2 |
又c=
| 5 |
| x2 |
| 4 |
| y2 |
| 1 |
| op |
| e1 |
| e2 |
点P是双曲线C上的点,
所以
| (2m+n)2 |
| 4 |
故答案为:4mn=1.
点评:本题主要考查了双曲线的简单性质.考查了向量的综合应用,学生分析问题和解决问题的能力.

练习册系列答案
相关题目
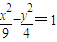 ,伸缩比λ=2,求C1关于原点“伸缩变换”后所得曲线C2的方程;
,伸缩比λ=2,求C1关于原点“伸缩变换”后所得曲线C2的方程;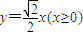 ,如果椭圆C1:
,如果椭圆C1: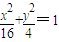 经“伸缩变换”后得到椭圆C2,若射线l与椭圆C1、C2分别交于两点A、B,且
经“伸缩变换”后得到椭圆C2,若射线l与椭圆C1、C2分别交于两点A、B,且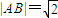 ,求椭圆C2的方程;
,求椭圆C2的方程;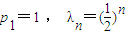 ,求数列{pn}的通项公式pn.
,求数列{pn}的通项公式pn.