题目内容
设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6, 且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(1)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(2)记 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求 的分布列及期望.
的分布列及期望.
(1)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(2)记
 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求 的分布列及期望.
的分布列及期望.(1)0.8;(2)2.4
试题分析:(1)因为每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,所以要求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率可以利用对立事件来解决,即1减去甲、乙都没购买的概率(1-0.5)(1-0.6),即可得所求的结论.
(2)由(1)可得每1位顾客至少购买甲、乙两种商品中的一种的概率为0.8.所以对三位顾客中至少购买甲、乙两种商品中的一种的人数的分为0,1,2,3四种情况.利用几何概型可求得相应的概率,再利用数学期望的公式即可得结论.
试题解析:
(1)

(2)
 取值有0、1、2、3
取值有0、1、2、3


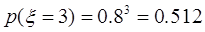
分布列为
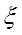 | 0 | 1 | 2 | 3 |
 | 0.008 | 0.096 | 0.384 | 0.512 |
E(
 )=3×0.8=2.4
)=3×0.8=2.4
练习册系列答案
相关题目
 道备选试验考查题中一次随机抽取
道备选试验考查题中一次随机抽取 题,并按照题目要求独立完成全部实验操作.规定:至少正确完成其中
题,并按照题目要求独立完成全部实验操作.规定:至少正确完成其中 题便通过考查.已知
题便通过考查.已知 题能正确完成,
题能正确完成, ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响. 和文科考生乙正确完成题数
和文科考生乙正确完成题数 的概率分布列,并计算各自的数学期望;
的概率分布列,并计算各自的数学期望; 为取出的3枝里一等品的枝数,求
为取出的3枝里一等品的枝数,求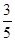 .
. ,服用B有效的概率为
,服用B有效的概率为 .
. ,道路C,E上下班时间往返出现拥堵的概率都是
,道路C,E上下班时间往返出现拥堵的概率都是 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.
 的分布列如下:
的分布列如下:

 ( )
( ) 后放入乙盒,再从乙盒中任取一小球,记下号码
后放入乙盒,再从乙盒中任取一小球,记下号码 .
.  的概率;
的概率; ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望.