题目内容
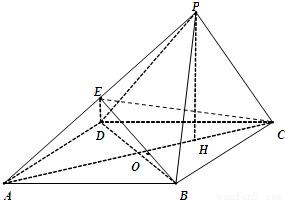
已知四棱锥P-ABCD的底面是菱形.∠BCD=60°,AB=PB=PD=2,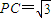 ,AC与BD交于O点,E,H分别为PA,OC的中点.
,AC与BD交于O点,E,H分别为PA,OC的中点.(Ⅰ)求证:PC∥平面BDE;
(Ⅱ)求证:PH⊥平面ABCD;
(Ⅲ)求直线CE与平面PAB所成角的正弦值.
【答案】分析:(Ⅰ)因为E,O分别为PA,AC的中点,所以EO∥PC.由此能够证明PC∥平面BDE.
(Ⅱ)连接OP,因为PB=PD,所以OP⊥BD.在菱形ABCD中,BD⊥AC,又因为OP∩AC=O,所以BD⊥平面PAC.又PH?平面PAC,所以BD⊥PH.由此能够证明PH⊥平面ABCD.
(Ⅲ)过点O作OZ∥PH,所以OZ⊥平面ABCD.以O为原点,OA,OB,OZ所在直线为x,y,z轴,建立空间直角坐标系.得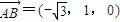 ,
,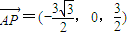 ,
,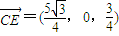 .设
.设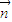 =(x,y,z)是平面PAB的一个法向量,由
=(x,y,z)是平面PAB的一个法向量,由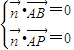 ,得
,得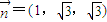 .由此能求出直线CE与平面PAB所成角的正弦值.
.由此能求出直线CE与平面PAB所成角的正弦值.
解答:(Ⅰ)证明:因为E,O分别为PA,AC的中点,
所以EO∥PC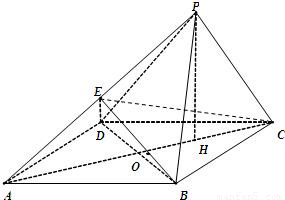
又EO?平面BDE,PC?平面BDE.
所以PC∥平面BDE.
(Ⅱ)证明:连接OP,
因为PB=PD,
所以OP⊥BD.
在菱形ABCD中,BD⊥AC,
又因为OP∩AC=O,所以BD⊥平面PAC.
又PH?平面PAC,所以BD⊥PH.
在直角三角形POB中,OB=1,PB=2,所以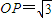 .
.
又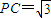 ,H为OC的中点,所以PH⊥OC.
,H为OC的中点,所以PH⊥OC.
又因为BD∩OC=O
所以PH⊥平面ABCD.
(Ⅲ)解:过点O作OZ∥PH,所以OZ⊥平面ABCD.
如图,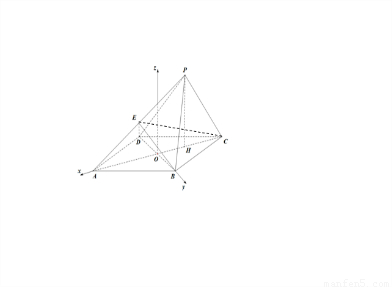 以O为原点,OA,OB,OZ所在直线为x,y,z轴,建立空间直角坐标系.
以O为原点,OA,OB,OZ所在直线为x,y,z轴,建立空间直角坐标系.
可得,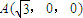 ,B(0,1,0),
,B(0,1,0),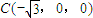 ,
,
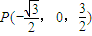 ,
,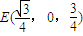 .
.
所以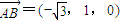 ,
, ,
,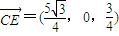 .
.
设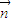 =(x,y,z)是平面PAB的一个法向量,
=(x,y,z)是平面PAB的一个法向量,
则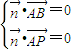 ,即
,即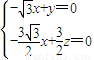 ,
,
令x=1,则 ..
..
设直线CE与平面PAB所成的角为θ,
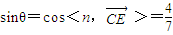 .
.
所以直线CE与平面PAB所成角的正弦值为 .
.
点评:本题考查直线和平面平行、直线和平面垂直的证明方法和求直线与平面在所成角的正弦值.解题时要认真审题,仔细解答,注意合理地进行等价转化.
(Ⅱ)连接OP,因为PB=PD,所以OP⊥BD.在菱形ABCD中,BD⊥AC,又因为OP∩AC=O,所以BD⊥平面PAC.又PH?平面PAC,所以BD⊥PH.由此能够证明PH⊥平面ABCD.
(Ⅲ)过点O作OZ∥PH,所以OZ⊥平面ABCD.以O为原点,OA,OB,OZ所在直线为x,y,z轴,建立空间直角坐标系.得
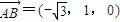 ,
,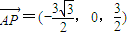 ,
,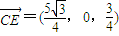 .设
.设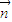 =(x,y,z)是平面PAB的一个法向量,由
=(x,y,z)是平面PAB的一个法向量,由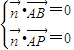 ,得
,得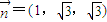 .由此能求出直线CE与平面PAB所成角的正弦值.
.由此能求出直线CE与平面PAB所成角的正弦值.解答:(Ⅰ)证明:因为E,O分别为PA,AC的中点,
所以EO∥PC

又EO?平面BDE,PC?平面BDE.
所以PC∥平面BDE.
(Ⅱ)证明:连接OP,
因为PB=PD,
所以OP⊥BD.
在菱形ABCD中,BD⊥AC,
又因为OP∩AC=O,所以BD⊥平面PAC.
又PH?平面PAC,所以BD⊥PH.
在直角三角形POB中,OB=1,PB=2,所以
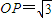 .
.又
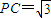 ,H为OC的中点,所以PH⊥OC.
,H为OC的中点,所以PH⊥OC.又因为BD∩OC=O
所以PH⊥平面ABCD.
(Ⅲ)解:过点O作OZ∥PH,所以OZ⊥平面ABCD.
如图,
 以O为原点,OA,OB,OZ所在直线为x,y,z轴,建立空间直角坐标系.
以O为原点,OA,OB,OZ所在直线为x,y,z轴,建立空间直角坐标系.可得,
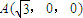 ,B(0,1,0),
,B(0,1,0),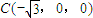 ,
,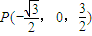 ,
,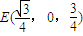 .
.所以
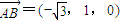 ,
, ,
,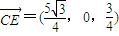 .
.设
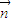 =(x,y,z)是平面PAB的一个法向量,
=(x,y,z)是平面PAB的一个法向量,则
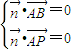 ,即
,即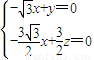 ,
,令x=1,则
 ..
..设直线CE与平面PAB所成的角为θ,
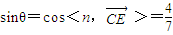 .
.所以直线CE与平面PAB所成角的正弦值为
 .
.点评:本题考查直线和平面平行、直线和平面垂直的证明方法和求直线与平面在所成角的正弦值.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
 如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.
如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点. 如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点.
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点. 已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE.
已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE. 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.