题目内容
设数列{an}的前n项和为Sn,点P(Sn,an)在直线(2-m)x+2my-m-2=0上,其中m为常数,且m>0.(Ⅰ)求证:{an}是等比数列,并求其通项an;
(Ⅱ)若数列{an}的公比q=f(m),数列{bn}满足b1=a1,bn=f(bn-1),(n∈N+,n≥2),求证:
 是等差数列,并求bn;
是等差数列,并求bn;(Ⅲ)设数列{cn}满足cn=bnbn+1,Tn为数列{cn}的前n项和,且存在实数T满足Tn≥T,(n∈N+)求T的最大值.
【答案】分析:(Ⅰ)由题设知(2-m)Sn+2man-m-2=0,当n=1时,a1=S1,(2-m)a1+2ma1-m-2=0,a1=1,当n≥2时,(2-m)Sn-1+2man-1-m-2=0,
两式相减得(2+m)an=2man-1,由此能求出其通项an;
(Ⅱ)由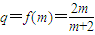 ,知
,知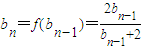 ,
,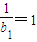 ,由此能证明
,由此能证明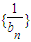 成等差数列;
成等差数列;
(Ⅲ)由{cn}满足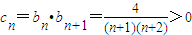 ,知Tn递增.
,知Tn递增.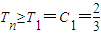 ,要满足Tn≥T对任意n∈N+都成立,
,要满足Tn≥T对任意n∈N+都成立,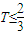 .由此能求出T的最大值.
.由此能求出T的最大值.
解答:解:(Ⅰ)∵点P(Sn,an)在直线(2-m)x+2my-m-2=0上,
∴(2-m)Sn+2man-m-2=0*(1分)
当n=1时,a1=S1,∴(2-m)a1+2ma1-m-2=0,
∴a1(m+2)=m+2∴a1=1,(2分)
当n≥2时,由*式知(2-m)Sn-1+2man-1-m-2=0**,
两式相减得(2+m)an=2man-1∵m>0∴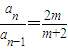 ,
,
∴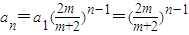 ,
,
又当n=1时也适合,∴{an}是等比数列,
通项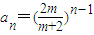 ;(5分)
;(5分)
(Ⅱ)由Ⅰ知 ,
,
∴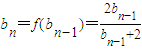 ,
,
∴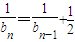
即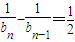 ,又
,又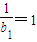 也适合,
也适合,
∴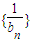 成等差数列,(7分)
成等差数列,(7分)
其通项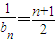 ,∴
,∴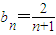 (9分)
(9分)
(Ⅲ)∵{cn}满足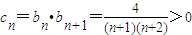 Tn为数列{cn}的前n项和,
Tn为数列{cn}的前n项和,
∴{Tn}是递增娄数列;(11分)
∴ ,要满足Tn≥T对任意n∈N+都成立,
,要满足Tn≥T对任意n∈N+都成立,
∴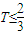 .∴T的最大值为
.∴T的最大值为 .(13分)
.(13分)
点评:本题考查数列的性质和应用,解题时要注意公式的合理运用,挖掘题设中的陷含条件.
两式相减得(2+m)an=2man-1,由此能求出其通项an;
(Ⅱ)由
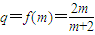 ,知
,知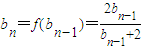 ,
,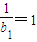 ,由此能证明
,由此能证明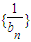 成等差数列;
成等差数列;(Ⅲ)由{cn}满足
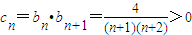 ,知Tn递增.
,知Tn递增.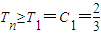 ,要满足Tn≥T对任意n∈N+都成立,
,要满足Tn≥T对任意n∈N+都成立,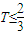 .由此能求出T的最大值.
.由此能求出T的最大值.解答:解:(Ⅰ)∵点P(Sn,an)在直线(2-m)x+2my-m-2=0上,
∴(2-m)Sn+2man-m-2=0*(1分)
当n=1时,a1=S1,∴(2-m)a1+2ma1-m-2=0,
∴a1(m+2)=m+2∴a1=1,(2分)
当n≥2时,由*式知(2-m)Sn-1+2man-1-m-2=0**,
两式相减得(2+m)an=2man-1∵m>0∴
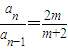 ,
,∴
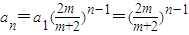 ,
,又当n=1时也适合,∴{an}是等比数列,
通项
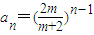 ;(5分)
;(5分)(Ⅱ)由Ⅰ知
 ,
,∴
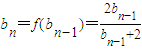 ,
,∴
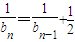
即
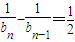 ,又
,又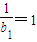 也适合,
也适合,∴
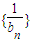 成等差数列,(7分)
成等差数列,(7分)其通项
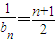 ,∴
,∴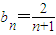 (9分)
(9分)(Ⅲ)∵{cn}满足
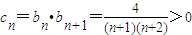 Tn为数列{cn}的前n项和,
Tn为数列{cn}的前n项和,∴{Tn}是递增娄数列;(11分)
∴
 ,要满足Tn≥T对任意n∈N+都成立,
,要满足Tn≥T对任意n∈N+都成立,∴
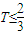 .∴T的最大值为
.∴T的最大值为 .(13分)
.(13分)点评:本题考查数列的性质和应用,解题时要注意公式的合理运用,挖掘题设中的陷含条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目