题目内容
已知f(x)=ax2+2bx+4c(a,b,c∈R)(1)若a+c=0,f(x)在[-2,2]上的最大值为
| 2 |
| 3 |
| 1 |
| 2 |
| b |
| a |
(2)当b=4,c=
| 3 |
| 4 |
(3)若f(x)同时满足下列条件:①a>0;②当|x|≤2时,有|f(x)|≤2;③当|x|≤1时,f(x)最大值为2,求f(x)的解析式.
分析:(1)利用反证法证明,若a等于0,得到c也等于0,所以f(x)等于2bx,得到f(2)与f(-2)互为相反数,不合题意;若a不为0,由a+c=0,解得c=-a,代入f(x)中,求出二次函数的对称轴,假设对称轴小于-2或大于2,即可得到对称轴在区间的左外侧或右外侧,得到f(x)为单调函数,函数的最值在x=2,-2取到,把2和-2代入得到最值互为相反数,不合题意,所以假设错误,综上,得证;
(2)把b与c的值代入f(x)中,配方得到顶点式,由a小于0,得到函数有最大值,表示出这个最大值,当最大值大于5时,求出此时a的范围,又最大值小于-
,M(a)是方程ax2+8x+3=5的较小根,利用求根公式求出M(a)即可判断出M(a)小于
;当最大值小于等于5时,求出此时a的范围,最大值大于-
,M(a)是方程ax2+8x+3=-5的较大根,根据求根公式求出M(a)即可判断M(a)小于等于
,又
大于
,即可得到M(a)的最大值;
(3)求出f(x)的导函数,由a大于0,求出函数有最大值让其等于2,得到a与b的关系式,由-2≤f(0)=4a=4a+4b+4c-4(a+b)=f(2)-4≤2-4=-2,得c的值,又因为|f(x)|≤2,所以f(x)≥-2=f(0),即可得到x=0时,函数取得最小值,表示出对称轴让其等于0,即可求得b的值,进而求出a的值,把a,b和c的值代入即可确定出f(x)的解析式.
(2)把b与c的值代入f(x)中,配方得到顶点式,由a小于0,得到函数有最大值,表示出这个最大值,当最大值大于5时,求出此时a的范围,又最大值小于-
| 4 |
| a |
| 1 |
| 2 |
| 4 |
| a |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
(3)求出f(x)的导函数,由a大于0,求出函数有最大值让其等于2,得到a与b的关系式,由-2≤f(0)=4a=4a+4b+4c-4(a+b)=f(2)-4≤2-4=-2,得c的值,又因为|f(x)|≤2,所以f(x)≥-2=f(0),即可得到x=0时,函数取得最小值,表示出对称轴让其等于0,即可求得b的值,进而求出a的值,把a,b和c的值代入即可确定出f(x)的解析式.
解答:解:(1)若a=0,则c=0,f(x)=2bx,f(2)=4b,f(-2)=-4b,不合题意;
若a≠0时,由a+c=0,得f(x)=ax2+2bx-4a,
对称轴为x=-
,假设
∈(-∞,-2)∪(2,+∞),
区间[-2,2]在对称轴的左外侧或右外侧,所以f(x)在[-2,2]上是单调函数,
则f(x)的最值必在x=2,x=-2处取到,
f(2)=4b,f(-2)=-4b,f(2)+f(-2)=0≠
+(-
)=
,
所以假设错误,则|
|≤2,
综上,得到|
|≤2;
(2)
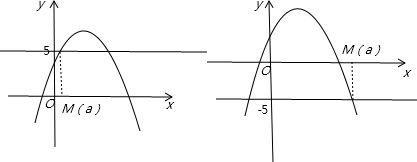
把b=4,c=
代入得:f(x)=ax2+8x+3=a(x+
)2+3-
,
∵a<0,所以f(x)max=3-
①当3-
>5,即-8<a<0时,
M(a)满足:-8<a<0且0<M(a)<-
,
所以M(a)是方程ax2+8x+3=5的较小根,
则M(a)=
=
<
=
;
②当3-
≤5即a≤-8时,此时M(a)≥-
,
所以M(a)是ax2+8x+3=-5的较大根,
则M(a)=
=
≤
=
,
当且经当a=-8时取等号,
由于
>
,因此当且经当a=-8时,M(a)取最大值
;
(3)求得f′(x)=2ax+2b,
∵a>0,∴f(x)max=2a+2b=2,即a+b=1,
则-2≤f(0)=4a=4a+4b+4c-4(a+b)=f(2)-4≤2-4=-2,
∴4c=-2,解得c=-
,
又∵|f(x)|≤2,所以f(x)≥-2=f(0)
∴f(x)在x=0处取得最小值,且0∈(-2,2),
∴-
=0,解得b=0,从而a=1,
∴f(x)=x2-2.
若a≠0时,由a+c=0,得f(x)=ax2+2bx-4a,
对称轴为x=-
| b |
| a |
| b |
| a |
区间[-2,2]在对称轴的左外侧或右外侧,所以f(x)在[-2,2]上是单调函数,
则f(x)的最值必在x=2,x=-2处取到,
f(2)=4b,f(-2)=-4b,f(2)+f(-2)=0≠
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
所以假设错误,则|
| b |
| a |
综上,得到|
| b |
| a |
(2)

把b=4,c=
| 3 |
| 4 |
| 4 |
| a |
| 16 |
| a |
∵a<0,所以f(x)max=3-
| 16 |
| a |
①当3-
| 16 |
| a |
M(a)满足:-8<a<0且0<M(a)<-
| 4 |
| a |
所以M(a)是方程ax2+8x+3=5的较小根,
则M(a)=
-8+
| ||
| 2a |
| 2 | ||
|
| 2 |
| 4 |
| 1 |
| 2 |
②当3-
| 16 |
| a |
| 4 |
| a |
所以M(a)是ax2+8x+3=-5的较大根,
则M(a)=
-8-
| ||
| 2a |
| 4 | ||
|
| 4 | ||
|
| ||
| 2 |
当且经当a=-8时取等号,
由于
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
(3)求得f′(x)=2ax+2b,
∵a>0,∴f(x)max=2a+2b=2,即a+b=1,
则-2≤f(0)=4a=4a+4b+4c-4(a+b)=f(2)-4≤2-4=-2,
∴4c=-2,解得c=-
| 1 |
| 2 |
又∵|f(x)|≤2,所以f(x)≥-2=f(0)
∴f(x)在x=0处取得最小值,且0∈(-2,2),
∴-
| 2b |
| 2a |
∴f(x)=x2-2.
点评:此题考查学生会利用反证法进行证明,考查了数形结合的数学思想,会求二次函数在闭区间上的最值,掌握二次函数的图象与性质,是一道综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目