题目内容
锐角三角形ABC中,若A=2B,A,B,C所对的边分别为a,b,c.则下列四个结论:
①sin3B=sin2C②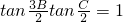 ③
③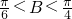 ④
④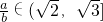
其中正确的是________.
②③④
分析:锐角三角形ABC中,由A=2B,可以由此解出B的取值范围,再由此范围对四个命题进行判断,得出真假
解答:∵锐角三角形ABC中,若A=2B
∴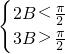
∴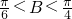
由于3B+C=π,故有sin3B=sinC,所以sin3B=sin2C不成立,①错误;
由于3B+C=π,可得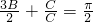 ,故有
,故有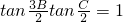 ,②正确;
,②正确;
由前解知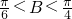 故③正确;
故③正确;
由于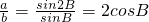 ,又
,又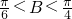 ,故有
,故有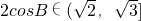 ,即得
,即得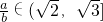 正确
正确
综上,②③④正确,
故答案为:②③④.
点评:本题考查命题的真假判断与应用,解题的关键是熟练掌握三角中的相关公式,对条件锐角三角形ABC中,A=2B的正确转化是本题的难点
分析:锐角三角形ABC中,由A=2B,可以由此解出B的取值范围,再由此范围对四个命题进行判断,得出真假
解答:∵锐角三角形ABC中,若A=2B
∴
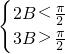
∴
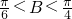
由于3B+C=π,故有sin3B=sinC,所以sin3B=sin2C不成立,①错误;
由于3B+C=π,可得
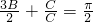 ,故有
,故有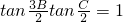 ,②正确;
,②正确;由前解知
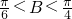 故③正确;
故③正确;由于
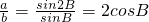 ,又
,又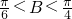 ,故有
,故有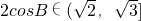 ,即得
,即得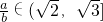 正确
正确综上,②③④正确,
故答案为:②③④.
点评:本题考查命题的真假判断与应用,解题的关键是熟练掌握三角中的相关公式,对条件锐角三角形ABC中,A=2B的正确转化是本题的难点

练习册系列答案
相关题目