题目内容

已知四棱锥P-ABCD的体积为V，AB∥CD，且AB：CD=2：3，点Q是PA的中点，则三棱锥Q-PBC的体积是（　　）
分析：画出几何体的图形，利用已知条件推出P-ABC 的体积，然后利用同底不等高，推出所求的体积．
解答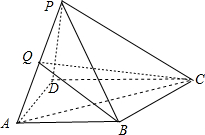：解：由题意如图，因为AB：CD=2：3，底面梯形高相同，棱锥的高相同，所以P-ABC的体积为
2
5
V．
在棱锥P-ABC中，底面PBC的面积相同，点Q是PA的中点，Q到底面PBC的距离是A到底面PBC距离的一半，
所以三棱锥Q-PBC的体积是棱锥P-ABC体积的一半，
所以三棱锥Q-PBC的体积是：
1
2
×
2
5
V=
1
5
V．
故选A．
点评：本题是基础题，考查几何体的体积的求法，注意距离的应用，线段平行之间的距离相等，考查计算能力．
练习册系列答案
相关题目
精英家教网如图，已知四棱锥P--ABC的底面ABCD为正方形，PA⊥平面ABCD，PA=AB=2，e为PC的中点，F为AD的中点．
（Ⅰ）证明EF∥平面PAB；
（Ⅱ）证明EF⊥平面PBC；
（III）点M是四边形ABCD内的一动点，PM与平面ABCD所成的角始终为45°，求动直线PM所形成的曲面与平面ABCD、平面PAB、平面PAD所围成几何体的体积．
精英家教网如图，已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，AB=BC=2CD=2，PB=PC，侧面PBC⊥底面ABCD，O是BC的中点．
（1）求证：PO⊥平面ABCD；
（2）求证：PA⊥BD
（3）若二面角D-PA-O的余弦值为
10
5
，求PB的长．
已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，E为BC中点，AE与BD交于O点，AB=BC=2CD=2，BD⊥PE．
（1）求证：平面PAE⊥平面ABCD； 
（2）若直线PA与平面ABCD所成角的正切值为
5
2
，PO=2，求四棱锥P-ABCD的体积．
如图，已知四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，∠DAB=∠ABC=90°，E是线段PC上一点，PC⊥平面BDE．
（Ⅰ）求证：BD⊥平面PAB．
（Ⅱ）若PA=4，AB=2，BC=1，求直线AC与平面PCD所成角的正弦值．
如图，已知四棱锥P--ABC的底面ABCD为正方形，PA⊥平面ABCD，PA=AB=2，e为PC的中点，F为AD的中点．
（Ⅰ）证明EF∥平面PAB；
（Ⅱ）证明EF⊥平面PBC；
（III）点M是四边形ABCD内的一动点，PM与平面ABCD所成的角始终为45°，求动直线PM所形成的曲面与平面ABCD、平面PAB、平面PAD所围成几何体的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网