题目内容
如果实数x,y满足
|
分析:画出满足约束条件
的平面区域,求出各个角点的坐标,根据对任意的正数a,b,不等式ax+by≤1恒成立,构造关于a,b的不等式组,结合不等式的基本性质,即可得到a+b的取值范围.
|
解答: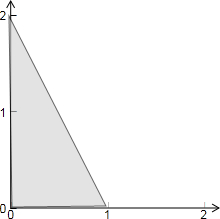 解:满足约束条件
解:满足约束条件
的平面区域如下图所示,
由于对任意的正数a,b,不等式ax+by≤1恒成立,
又ax+by的最大值在右上边界处取到,即在点(0,2)与点(1,0)处取到
∴
即
又∵a>0,b>0,
∴a<a+b≤
故a+b的取值范围是(0,
]
故答案为:(0,
]
 解:满足约束条件
解:满足约束条件
|
由于对任意的正数a,b,不等式ax+by≤1恒成立,
又ax+by的最大值在右上边界处取到,即在点(0,2)与点(1,0)处取到
∴
|
|
又∵a>0,b>0,
∴a<a+b≤
| 3 |
| 2 |
故a+b的取值范围是(0,
| 3 |
| 2 |
故答案为:(0,
| 3 |
| 2 |
点评:本题考查的知识点是简单线性规划,其中根据约束条件,画出满足约束条件的可行域并求出各角点的坐标,是解答此类问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目