Question

如果实数x，y满足

x-y+2≥0 x+y-4≥0 2x-y-5≤0

，则z=|x+2y+4|的最大值

29

．

Answer 1

分析：先确定平面区域，再求

|x+2y+4|

5

的最大值，从而可求z=|x+2y+4|的最大值．

解答：解：不等式表示的平面区域为

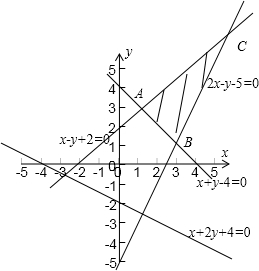
其中C的坐标由

x-y+2=0 2x-y-5=0

，可得

x=7 y=9

，即C（7，9）
先求

|x+2y+4|

5

的最大值
由图可知，C到直线x+2y+4=0的距离为

|7+18+4|

5

=

29

5

∴z=|x+2y+4|的最大值为29
故答案为：29

点评：本小题主要考查线性规划问题，以及简单的转化思想和数形结合的思想，属中档题．