题目内容
(2010•天津模拟)如果实数x、y满足
,目标函数z=kx+y的最大值为12,最小值3,那么实数k的值为
|
2
2
.分析:先画出可行域,得到角点坐标.再通过对斜率的分类讨论得到最大最小值点,与原题相结合即可得到答案.
解答: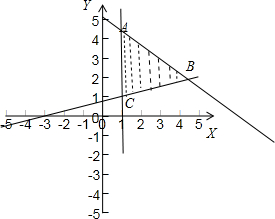 解:可行域如图,
解:可行域如图,
得:A(1,4.4),B(5,2),C(1,1).
又l1:x-4y+3=0的斜率k1=
;
l2:3x+5y-25=0的斜率k2=-
.
①当-k<-
时,C为最小值点,B为最大值点;
有:5k+2=12,且k+1=3,
⇒k=2;
②当-k>
时,C为最小值点,A为最大值点;
有:k+4.4=12,且k+1=3,
⇒k无解;
③当-
<-k<0时,C为最小值点,A为最大值点;
有:k+4.4=12,且k+1=3,
⇒k无解;
④当-k∈(0,
)时,C为最小值点,A为最大值点.
有:k+4.4=12,且k+1=3,
⇒k无解;
∴由①得k=2,其它情况的解都不符合要求.
故k=2.
故答案为:2.
 解:可行域如图,
解:可行域如图,得:A(1,4.4),B(5,2),C(1,1).
又l1:x-4y+3=0的斜率k1=
| 1 |
| 4 |
l2:3x+5y-25=0的斜率k2=-
| 3 |
| 5 |
①当-k<-
| 3 |
| 5 |
有:5k+2=12,且k+1=3,
⇒k=2;
②当-k>
| 1 |
| 4 |
有:k+4.4=12,且k+1=3,
⇒k无解;
③当-
| 3 |
| 5 |
有:k+4.4=12,且k+1=3,
⇒k无解;
④当-k∈(0,
| 1 |
| 4 |
有:k+4.4=12,且k+1=3,
⇒k无解;
∴由①得k=2,其它情况的解都不符合要求.
故k=2.
故答案为:2.
点评:本题主要考查简单线性规划以及分类讨论思想.解决此类问题的关键是正确画出不等式组表示的可行域,将目标函数赋予几何意义.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 (2010•天津模拟)某几何体的三视图,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是
(2010•天津模拟)某几何体的三视图,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是