Question

【题目】设f′（x）是函数f（x）的导函数，且f′（x）＞2f（x）（x∈R），f（）=e（e为自然对数的底数），则不等式f（lnx）＜x2的解集为（　　）
A.（0，）
B.（0，）
C.（ ， ）
D.（ ， ）

Answer 1

【答案】B
【解析】可构造函数F（x）= ，
F′（x）=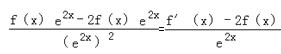
由f′（x）＞2f（x），可得F′（x）＞0，即有F（x）在R上递增．
不等式f（lnx）＜x2即为＜1，（x＞0），即＜1，x＞0．
即有F（）==1，即为F（lnx）＜F（），
由F（x）在R上递增，可得lnx＜ ， 解得0＜x＜ ．
故不等式的解集为（0，），
故选：B．
构造函数F（x）= ， 求出导数，判断F（x）在R上递增．原不等式等价为F（lnx）＜F（），运用单调性，可得lnx＜ ， 运用对数不等式的解法，即可得到所求解集。