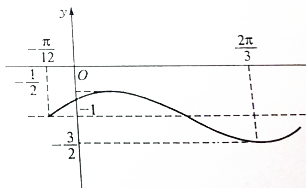
题目内容
18.计算:(0.027)${\;}^{\frac{1}{3}}$-(6$\frac{1}{4}$)${\;}^{\frac{1}{2}}$+256${\;}^{\frac{3}{4}}$+(2$\sqrt{2}$)${\;}^{\frac{2}{3}}$-3-1+π0=64$\frac{7}{15}$.分析 (0.027)${\;}^{\frac{1}{3}}$=$0.{3}^{3×\frac{1}{3}}$=0.3,(6$\frac{1}{4}$)${\;}^{\frac{1}{2}}$=$(\frac{25}{4})^{\frac{1}{2}}$=$\frac{5}{2}$,256${\;}^{\frac{3}{4}}$=${4}^{4×\frac{3}{4}}$=64,(2$\sqrt{2}$)${\;}^{\frac{2}{3}}$=$(\sqrt{2})^{3×\frac{2}{3}}$=2,3-1=$\frac{1}{3}$,π0=1;代入即可.
解答 解:(0.027)${\;}^{\frac{1}{3}}$=$0.{3}^{3×\frac{1}{3}}$=0.3,
(6$\frac{1}{4}$)${\;}^{\frac{1}{2}}$=$(\frac{25}{4})^{\frac{1}{2}}$=$\frac{5}{2}$,
256${\;}^{\frac{3}{4}}$=${4}^{4×\frac{3}{4}}$=64,
(2$\sqrt{2}$)${\;}^{\frac{2}{3}}$=$(\sqrt{2})^{3×\frac{2}{3}}$=2,
3-1=$\frac{1}{3}$,π0=1;
故(0.027)${\;}^{\frac{1}{3}}$-(6$\frac{1}{4}$)${\;}^{\frac{1}{2}}$+256${\;}^{\frac{3}{4}}$+(2$\sqrt{2}$)${\;}^{\frac{2}{3}}$-3-1+π0
=0.3-$\frac{5}{2}$+64+2-$\frac{1}{3}$+1=64$\frac{7}{15}$;
故答案为:64$\frac{7}{15}$.
点评 本题考查了有理指数幂的化简与运算.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | lg2 | B. | 3(1-lg3) | C. | lg5-1 | D. | -lg5-1 |
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | ±$\frac{7}{5}$ | D. | $\frac{7}{5}$ |