题目内容
设函数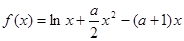 (
(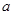 为常数)
为常数)
(Ⅰ)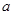 =2时,求
=2时,求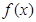 的单调区间;
的单调区间;
(Ⅱ)当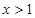 时,
时,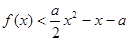 ,求
,求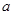 的取值范围
的取值范围
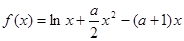 (
(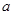 为常数)
为常数) (Ⅰ)
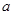 =2时,求
=2时,求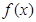 的单调区间;
的单调区间;(Ⅱ)当
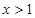 时,
时,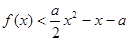 ,求
,求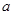 的取值范围
的取值范围 ①在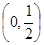 ,
,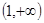 上单调递增,在
上单调递增,在 上单调递减,②
上单调递减,②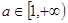
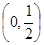 ,
,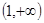 上单调递增,在
上单调递增,在 上单调递减,②
上单调递减,②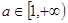
试题分析:(Ⅰ)求函数的导数,研究二次函数的零点情况,确定导函数的正负取值区间,进一步确定原函数的单调性 (Ⅱ)先把原不等式等价转化为
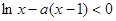 在
在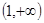 上恒成立 求其导函数,分类研究原函数的单调性及值域变化确定
上恒成立 求其导函数,分类研究原函数的单调性及值域变化确定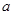 的取值范围
的取值范围 试题解析:(Ⅰ)
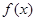 的定义域为
的定义域为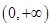 ,
,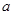 =2时,
=2时,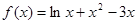 ,
, ,
,当
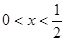 ,解得
,解得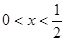 或
或 ;当
;当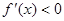 ,解得
,解得 ,
,∴函数
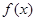 在
在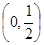 ,
,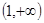 上单调递增,在
上单调递增,在 上单调递减 5分
上单调递减 5分(Ⅱ)
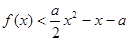 等价于
等价于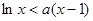 在
在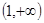 上恒成立,
上恒成立,即
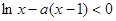 在
在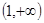 上恒成立
上恒成立 设
 ,则
,则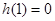 ,
,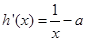
①若
 ,
,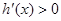 ,函数
,函数 为增函数,且向正无穷趋近,显然不满足条件;
为增函数,且向正无穷趋近,显然不满足条件;②若
 ,则
,则 ∈
∈ 时,
时, 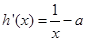
 0恒成立,
0恒成立,∴
 在
在 上为减函数,
上为减函数, ∴
 在
在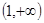 上恒成立,
上恒成立,即
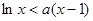 在
在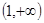 上恒成立;
上恒成立;③若
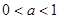 ,则
,则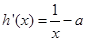 =0时,
=0时, ,∴
,∴ 时,
时,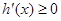 ,
,∴
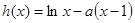 在
在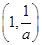 上为增函数,
上为增函数,当
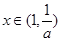 时,
时,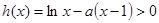 ,不能使
,不能使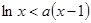 在
在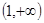 上恒成立
上恒成立 综上,
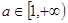 12分
12分
练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
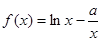 (
(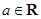 ).
).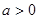 时,判断
时,判断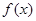 在定义域上的单调性;
在定义域上的单调性;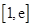 上的最小值为
上的最小值为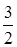 ,求
,求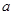 的值;
的值;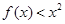 在
在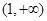 上恒成立,试求
上恒成立,试求
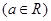 .
.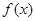 在
在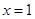 处的切线垂直于直线
处的切线垂直于直线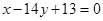 ,求该点的切线方程,并求此时函数
,求该点的切线方程,并求此时函数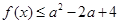 对任意的
对任意的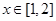 恒成立,求实数
恒成立,求实数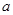 的取值范围.
的取值范围.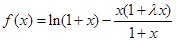 .
.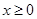 时,
时,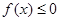 ,求
,求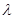 的最小值;
的最小值;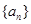 的通项
的通项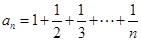 ,证明:
,证明: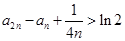 .
. >f(x),则 ( )
>f(x),则 ( ) f(0)
f(0)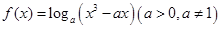 在区间
在区间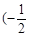 ,0)内单调递增,则
,0)内单调递增,则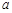 取值范围是( )
取值范围是( )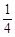 ,1)
,1)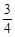 ,1)
,1)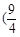 ,
,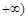
 )
) ,则下列结论正确的是( )
,则下列结论正确的是( ) 在
在 上恰有一个零点
上恰有一个零点 上恰有一个零点
上恰有一个零点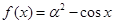 ,则
,则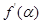 等于( )
等于( ) 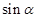
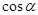
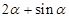
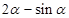
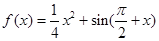 ,
,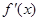 为
为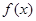 的导函数,则
的导函数,则