题目内容
1.在△ABC中,角A,B,C所对的边分别为a,b,c,已知∠A=45°,a=10,b=5,求∠B.分析 利用正弦定理解出即可.
解答 解:∵∠A=45°,a=10,b=5,
∴$\frac{a}{sinA}=\frac{b}{sinB}$,即$\frac{10}{sin4{5}^{°}}=\frac{5}{sinB}$,化为sinB=$\frac{\sqrt{2}}{4}$,
又b<a,
∴B为锐角,
∴B=arcsin$\frac{\sqrt{2}}{4}$.
点评 本题考查了正弦定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
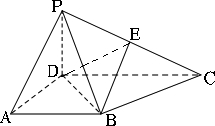 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,AD⊥CD,且AB=AD=PD=1,CD=2,E为PC的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,AD⊥CD,且AB=AD=PD=1,CD=2,E为PC的中点.