题目内容
数列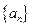 的各项均为正数,
的各项均为正数,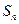 为其前
为其前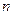 项和,对于任意
项和,对于任意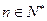 ,总有
,总有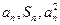 成等差数列.
成等差数列.
(1)求数列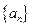 的通项公式;
的通项公式;
(2)设数列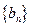 的前
的前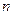 项和为
项和为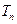 ,且
,且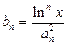 ,求证:对任意实数
,求证:对任意实数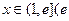 是常数,
是常数,
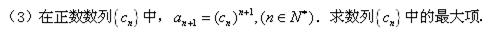
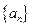 的各项均为正数,
的各项均为正数,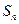 为其前
为其前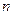 项和,对于任意
项和,对于任意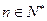 ,总有
,总有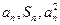 成等差数列.
成等差数列.(1)求数列
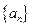 的通项公式;
的通项公式;(2)设数列
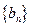 的前
的前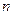 项和为
项和为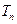 ,且
,且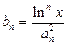 ,求证:对任意实数
,求证:对任意实数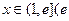 是常数,
是常数,
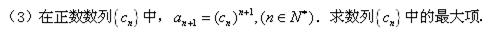
(1)
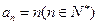
(2)证明略
(3)
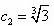
解:由已知:对于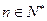 ,总有
,总有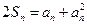 成立………(1)
成立………(1)
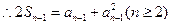 (2) ………………………………2分
(2) ………………………………2分
(1)—(2)得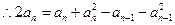
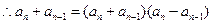
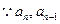 均为正数,
均为正数, 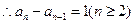
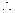 数列
数列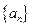 是公差为1的等差数列 ………………………………3分
是公差为1的等差数列 ………………………………3分
又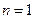 时,
时,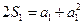 ,解得
,解得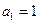
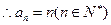 ……………………………………………………4分
……………………………………………………4分
(2)证明: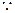 对任意实数
对任意实数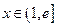 和任意正整数
和任意正整数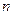 ,总有
,总有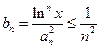 ……6分
……6分
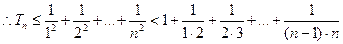
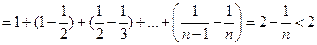 ………………8分
………………8分
(3)解:由已知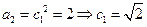
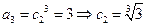 ,
,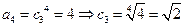 ,
,
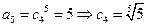
易得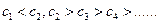
猜想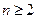 时,
时,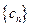 是递减数列 …………………………………………10分
是递减数列 …………………………………………10分
令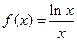 ,则
,则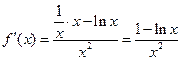
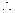 当
当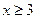 时,
时,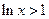 ,则
,则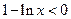 ,即
,即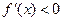
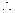
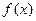 在
在 内为单调递减函数,
内为单调递减函数,
由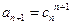 知
知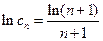

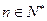 ,总有
,总有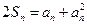 成立………(1)
成立………(1)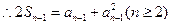 (2) ………………………………2分
(2) ………………………………2分(1)—(2)得
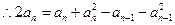
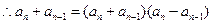
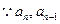 均为正数,
均为正数, 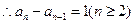
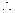 数列
数列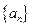 是公差为1的等差数列 ………………………………3分
是公差为1的等差数列 ………………………………3分又
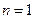 时,
时,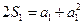 ,解得
,解得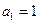
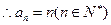 ……………………………………………………4分
……………………………………………………4分(2)证明:
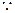 对任意实数
对任意实数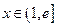 和任意正整数
和任意正整数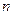 ,总有
,总有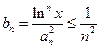 ……6分
……6分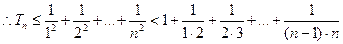
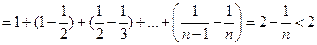 ………………8分
………………8分(3)解:由已知
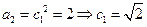
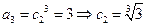 ,
,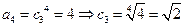 ,
,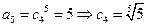
易得
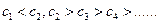
猜想
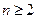 时,
时,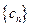 是递减数列 …………………………………………10分
是递减数列 …………………………………………10分令
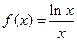 ,则
,则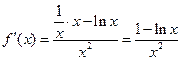
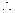 当
当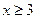 时,
时,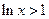 ,则
,则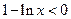 ,即
,即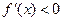
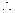
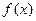 在
在 内为单调递减函数,
内为单调递减函数,由
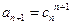 知
知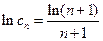


练习册系列答案
相关题目
 }的前
}的前 项和为
项和为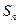 ,已知5
,已知5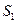 、2
、2 、
、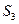 成等差数列.
成等差数列. ;
; -
-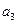 =3且
=3且 时,求
时,求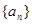 是等差数列,且
是等差数列,且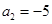 ,
,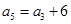 ,则
,则
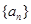 中,
中,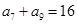 ,
,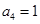 ,则
,则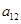 的值是 ( )
的值是 ( )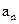 ﹜中,
﹜中, =
=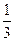 ,前n项和
,前n项和 满足
满足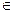 N*
N* )
)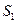 ,t(
,t(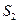 ), 3(
), 3(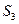 )成等差数列,求实数t的值。
)成等差数列,求实数t的值。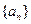 的公差
的公差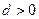 ,其前n项和为
,其前n项和为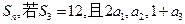 成等比数列。
成等比数列。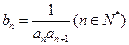 ,求数列
,求数列 的前n项和
的前n项和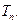
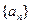 ,
,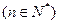 是等差数列,则有数列
是等差数列,则有数列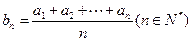 也为等差数列,类比上述性质,相应地:若数列
也为等差数列,类比上述性质,相应地:若数列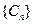 是等比数列,且
是等比数列,且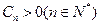 ,则有
,则有 _____ _____
_____ _____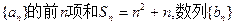 满足
满足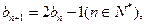 且
且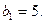
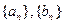 的通项公式;
的通项公式;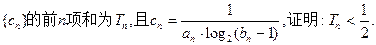
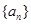 是等差数列,
是等差数列,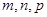 是互不相等的正整数,有正确的结论:
是互不相等的正整数,有正确的结论: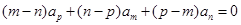 ,类比上述性质,相应地,若等比数列
,类比上述性质,相应地,若等比数列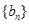 ,
,