题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)如果对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2) ![]() .
.
【解析】
(1)利用配方法化简函数,根据函数的定义域,换元得到t=![]() ∈[0,2],由二次函数的性质,即可求出函数的值域;(2)先利用对数运算化简不等式,换元,再通过分离参数法,转化为最值问题,利用基本不等式求出最值,即可求出实数
∈[0,2],由二次函数的性质,即可求出函数的值域;(2)先利用对数运算化简不等式,换元,再通过分离参数法,转化为最值问题,利用基本不等式求出最值,即可求出实数![]() 的取值范围.
的取值范围.
(1)h(x)=(4-2![]() )·
)·![]() =-2(
=-2(![]() -1)2+2,
-1)2+2,
因为x∈[1,4],所以t=![]() ∈[0,2],
∈[0,2],![]() ,
,
故函数h(x)的值域为[0,2].
(2)由f(x2)·f(![]() )>k·g(x),
)>k·g(x),
得(3-4![]() )(3-
)(3-![]() )>k·
)>k·![]() ,
,
令![]() ,因为x∈[1,4],所以t=
,因为x∈[1,4],所以t=![]() ∈[0,2],
∈[0,2],
所以(3-4t)(3-t)>k·t对一切t∈[0,2]恒成立,
①当t=0时,k∈R;
②当t∈(0,2]时,![]() 恒成立,
恒成立,
即![]() ,
,
因为![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时取等号,
时取等号,
所以![]() 的最小值为-3.所以k<-3.
的最小值为-3.所以k<-3.
综上,实数k的取值范围为(-∞,-3).

【题目】某公司为了解用户对其产品的满意度,从A、B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
A地区: | 62 | 73 | 81 | 92 | 95 | 85 | 74 | 64 | 53 | 76 |
78 | 86 | 95 | 66 | 97 | 78 | 88 | 82 | 76 | 89 | |
B地区: | 73 | 83 | 62 | 51 | 91 | 46 | 53 | 73 | 64 | 82 |
93 | 48 | 95 | 81 | 74 | 56 | 54 | 76 | 65 | 79 |
(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度的平均值及分散程度(不要求算出具体值,给出结论即可):

(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”,假设两地区用户的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率。
【题目】耐盐碱水稻俗称“海水稻”,是一种可以长在滩涂和盐碱地的水稻。还水稻的灌溉是将海水稀释后进行灌溉。某实验基础为了研究海水浓度![]() (
(![]() )对亩产量
)对亩产量![]() (吨)的影响,通过在试验田的种植实验,测得了某种还水稻的亩产量与海水浓度的数据如下表:
(吨)的影响,通过在试验田的种植实验,测得了某种还水稻的亩产量与海水浓度的数据如下表:
海水浓度 |
|
|
|
|
|
亩产量 |
|
|
|
|
|
绘制散点图发现,可用线性回归模型拟合亩产量![]() 与海水浓度
与海水浓度![]() 之间的相关关系,用最小二乘法计算得
之间的相关关系,用最小二乘法计算得![]() 与
与![]() 之间的线性回归方程为
之间的线性回归方程为![]() .
.
(1)求出![]() 的值,并估算当浇灌海水浓度为8%时该品种的亩产量。
的值,并估算当浇灌海水浓度为8%时该品种的亩产量。
(2)①完成下列残差表:
海水浓度 |
|
|
|
|
|
亩产量 |
|
|
|
|
|
| |||||
残差 |
②统计学中常用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越大,模型拟合效果越好,如假设
越大,模型拟合效果越好,如假设![]() ,就说明预报变量
,就说明预报变量![]() 的差异有
的差异有![]() 是由解释变量
是由解释变量![]() 引起的.请计算相关指数
引起的.请计算相关指数![]() (精确到0.01),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的.
(精确到0.01),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的.
(附:残差公式![]() ,相关指数
,相关指数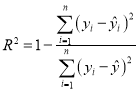 ,参考数据
,参考数据![]() )
)