题目内容
(本题满分16分)袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为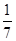 ,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用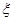 表示取球终止所需要的取球次数.
表示取球终止所需要的取球次数.
(1)求袋中原有白球的个数;
(2)求随机变量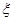 的概率分布;
的概率分布;
(3)求甲取到白球的概率.
【答案】
(1)袋中原有3个白球
(2)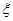 的分布列为:
的分布列为:
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
(3)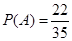
【解析】(1)设袋中原有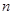 个白球,由题意知
个白球,由题意知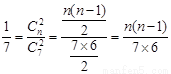 ……………3分
……………3分
∴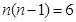 得
得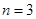 或
或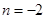 (舍去),即袋中原有3个白球.……………… 5分
(舍去),即袋中原有3个白球.……………… 5分
(2)由题意,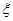 的可能取值为
的可能取值为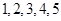
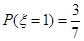 ;
;
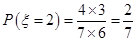 ;
;
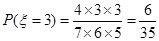 ;
; 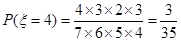 ;
;
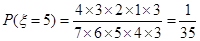 ……………………………………………10分
……………………………………………10分
所以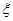 的分布列为:
的分布列为:
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
………………………………………………………………………………………… 12分
(3)因为甲先取,所以甲只有可能在第1次,第3次和第5次取球,记”甲取到白球”为事件 ,则
,则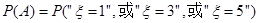
∵事件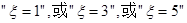 两两互斥,
两两互斥,
∴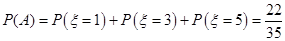 ……………………………… 16分
……………………………… 16分

练习册系列答案
相关题目
(本题满分16分)某家俱公司生产甲、乙两种型号的组合柜,每种柜的制造白坯时间、油漆时间及有关数据如下:
| 工艺要求 | 产品甲 | 产品乙 | 生产能力/(台/天) |
| 制白坯时间/天 | 6 | 12 | 120 |
| 油漆时间/天 | 8 | 4 | 64 |
| 单位利润/元 | 20 | 24 | |



 所在平面与正
所在平面与正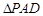 所在平面互相垂直,
所在平面互相垂直,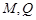 分别为
分别为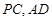 的中点.
的中点.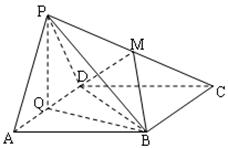
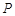 -
- 的体积;
的体积;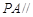 平面
平面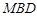 ;
;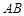 上是否存在一点
上是否存在一点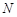 ,使得平面
,使得平面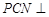 平面
平面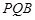 ?若存在,试指出点
?若存在,试指出点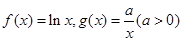 ,设
,设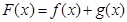
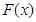 的单调区间;
的单调区间; )图像上任意一点
)图像上任意一点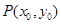 为切点的切线的斜率
为切点的切线的斜率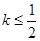 恒成立,求实数
恒成立,求实数 的最小值;
的最小值;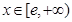 都有
都有 成立,求实数
成立,求实数