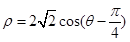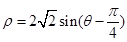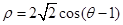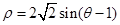题目内容
在平面直角坐标系中,以原点为极点,x轴正半轴为极轴建立极坐标系,已知抛物线C的极坐标方程为ρcos2θ=4sin θ(ρ≥0),直线l的参数方程为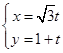 (t为参数),设直线l与抛物线C的两交点为A,B,点F为抛物线C的焦点,则|AF|+|BF|=__________.
(t为参数),设直线l与抛物线C的两交点为A,B,点F为抛物线C的焦点,则|AF|+|BF|=__________.
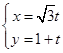 (t为参数),设直线l与抛物线C的两交点为A,B,点F为抛物线C的焦点,则|AF|+|BF|=__________.
(t为参数),设直线l与抛物线C的两交点为A,B,点F为抛物线C的焦点,则|AF|+|BF|=__________.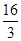
试题分析:抛物线
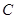 的极坐标方程为
的极坐标方程为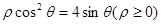 ,即
,即 ,焦点
,焦点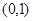 ,标准方程
,标准方程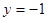 ,直线
,直线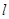 的参数方程为
的参数方程为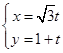 ,即
,即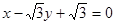 ,
,把直线方程代入抛物线
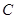 的方程可得
的方程可得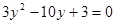 ,所以
,所以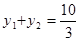 ,
,由抛物线的定义可得|AF|+|BF|=
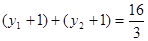 .
.点评:本题主要考查把极坐标方程化为直角坐标方程的方法,把参数方程化为普通方程的方法,抛物线的定义以及标准方程的应用,属于基础题.

练习册系列答案
相关题目
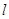 的方程为
的方程为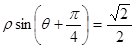 ,则点
,则点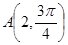 到直线
到直线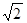
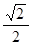
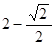
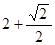
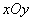 内,直线
内,直线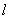 的参数方程为
的参数方程为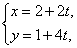
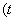 为参数
为参数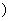 .以
.以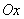 为极轴建立极坐标系,圆
为极轴建立极坐标系,圆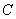 的极坐标方程为
的极坐标方程为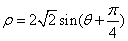 .判断直线
.判断直线 化成直角坐标为
化成直角坐标为 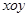 中,圆
中,圆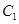 的参数方程为
的参数方程为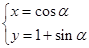 (
(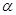 为参数)在极坐标系(与直角坐标系
为参数)在极坐标系(与直角坐标系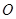 为极点,以
为极点,以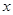 轴的正半轴为极轴)中,圆
轴的正半轴为极轴)中,圆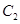 的极坐方程为
的极坐方程为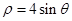 ,则
,则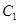 的参数方程为
的参数方程为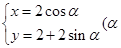 为参数),M为
为参数),M为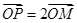 ,点P的轨迹为曲线
,点P的轨迹为曲线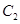 .已知在以O为极点,x轴的正半轴为极轴的极坐标系中,射线
.已知在以O为极点,x轴的正半轴为极轴的极坐标系中,射线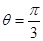 与
与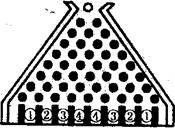
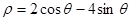 ,试求:
,试求: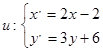 得到曲线
得到曲线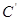 ,则曲线
,则曲线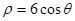 ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为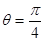 ,曲线C1,C2相交于A,B两点
,曲线C1,C2相交于A,B两点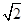 为半径的圆在以直角坐标系的原点为极点,以ox为极轴的极坐标系中对应的极坐标方程为( )
为半径的圆在以直角坐标系的原点为极点,以ox为极轴的极坐标系中对应的极坐标方程为( )