题目内容
如图所示，在△ABC中，∠B=60°，∠C=45°，高AD=| 3 |
分析：利用条件确定满足BM＜1对应的测度，然后利用几何概型公式求概率．
解答：解：因为∠B=60?，∠C=45?，所以∠BAC=75?．
在Rt△ABD中，AD=
，∠B=60?，所以BD=
=1，∠BAD=30?．
即事件N为“在∠BAC内作射线AM交BC于点M，使BM＜1”，
则可得∠BAM＜∠BAD时 事件N发生，
由几何概型的概率公式得P(N)=
=
．
在Rt△ABD中，AD=
| 3 |
| AD |
| tan60? |
即事件N为“在∠BAC内作射线AM交BC于点M，使BM＜1”，
则可得∠BAM＜∠BAD时 事件N发生，
由几何概型的概率公式得P(N)=
| 30? |
| 75? |
| 2 |
| 5 |
点评：本题主要考查了几何概型的概率公式，将所求的概率进行等价转化为等价的几何测度，是解决几何概型问题的关键．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
如图所示，在△ABC，已知
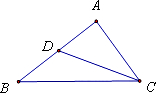如图所示，在△ABC中，点D是边AB的中点，则向量| DC |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
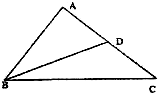如图所示，在△ABC中，∠B=60°，∠C=45°，高AD=
如图所示，在△ABC中，∠BAC=90°，∠ABC=60°，AD⊥BC于D，则