题目内容
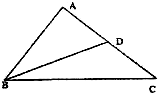 如图所示,在△ABC,已知AB=
如图所示,在△ABC,已知AB=4
| ||
| 3 |
| ||
| 6 |
| 5 |
(1)BC的长度;
(2)sinA的值.
分析:(1)取BC的中点E,则DE 是三角形ABC的中位线,∠DEB=π-B,△BDE中,由余弦定理可得BD2=ED2+EB2-2ED•EB cos(π-B),解出 BE,即可得到 BC 的值.
(2)在△ABC中,由余弦定理可求得AC的值,由正弦定理求得sinA的值.
(2)在△ABC中,由余弦定理可求得AC的值,由正弦定理求得sinA的值.
解答:解:(1)取BC的中点E,由于D是AC的中点,∴DE 是三角形ABC的中位线,故 DE=
,
且∠DEB=π-B,△BDE中,由余弦定理可得 BD2=ED2+EB2-2ED•EB cos(π-B),
∴5=
+BE2+2
•
•BE,解得 BE=1,或BE=-
(舍去),∴BC=2.
(2)在△ABC中,由余弦定理可得 AC2=AB2+BC2-2AB•BCcosB=
,
∴AC=
. 由
=
可得 sinA=
.
2
| ||
| 3 |
且∠DEB=π-B,△BDE中,由余弦定理可得 BD2=ED2+EB2-2ED•EB cos(π-B),
∴5=
| 8 |
| 3 |
2
| ||
| 3 |
| ||
| 6 |
| 7 |
| 3 |
(2)在△ABC中,由余弦定理可得 AC2=AB2+BC2-2AB•BCcosB=
| 28 |
| 3 |
∴AC=
2
| ||
| 3 |
| BC |
| sinA |
| AC |
| sinB |
| ||
| 14 |
点评:本题考查正弦定理,余弦定理的应用,诱导公式,求出AC的长度,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
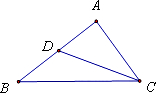 如图所示,在△ABC中,点D是边AB的中点,则向量
如图所示,在△ABC中,点D是边AB的中点,则向量| DC |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD= 如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则
如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=