题目内容
4.△ABC的三边长分别为|AC|=3,|BC|=4,|AB|=5,点P是△ABC内切圆上一点,求|PA|2+||PB|2+|PC|2的最小值与最大值.分析 以CA所在边为x轴建立直角坐标系,得内切圆方程为(x-1)2+(y-1)2=1,设P坐标为(x,y),化简要求的式子为22-2y,根据0≤y≤2,求得要求式子的值.
解答 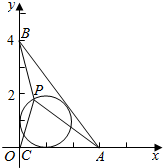 解:如图以C为原点,CA所在边为x轴建立直角坐标系,
解:如图以C为原点,CA所在边为x轴建立直角坐标系,
则A(3,0),B(0,4),C(0,0).
由直角△ABC,可得内切圆的半径r=$\frac{1}{2}$(3+4-5)=1,
得内切圆方程为(x-1)2+(y-1)2=1,即为x2+y2=2x+2y-1,
设P坐标为(x,y),
则|PA|2+|PB|2+|PC|2=(x-3)2+y2+x2+(y-4)2+x2+y2
=3x2+3y2-6x-8y+25=22-2y,
因为0≤y≤2,
所以22-2y∈[18,22].
即有P为(1,2)时,取得最小值18;
P为(1,0)时,取得最大值22.
点评 本题考查坐标法求最值的方法,考查直角三角形的内切圆的方程,以及平面上两点的距离公式的运用,属于中档题.

练习册系列答案
相关题目