题目内容
(1)不等式 对一切
对一切 R恒成立,求实数
R恒成立,求实数 的取值范围;
的取值范围;
(2)已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,求
,求 的解析式.
的解析式.
(1)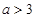 ;(2)
;(2)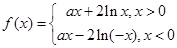 .
.
解析试题分析:(1)对二次项系数为参数 的一元二次不等式,解之前应先分
的一元二次不等式,解之前应先分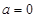 和
和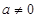 两种情况进行讨论,从而解得实数
两种情况进行讨论,从而解得实数 的取值范围;(2)此类问题需求
的取值范围;(2)此类问题需求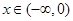 时的解析式,则设
时的解析式,则设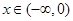 ,此时
,此时 ,根据
,根据 时的解析式得
时的解析式得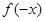 表达式,再由函数
表达式,再由函数 是定义在
是定义在 上的奇函数,可得
上的奇函数,可得 ,既得
,既得 的解析式.
的解析式.
试题解析:(1)当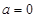 时,原不等式为
时,原不等式为 ,显然不对一切
,显然不对一切 R恒成立,则
R恒成立,则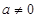 ;1分
;1分
当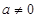 时,由不等式
时,由不等式 ,即
,即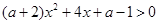 对一切
对一切 R恒成立,
R恒成立,
则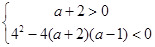 , 4分
, 4分
化简得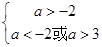 ,即
,即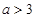 , 5分
, 5分
所以实数 的取值范围为
的取值范围为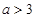 . 6分
. 6分
(2)由题意当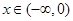 时,
时, ,所以
,所以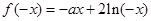 , 9分
, 9分
又因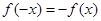 ,则
,则 , 12分
, 12分
所以 的解析式为
的解析式为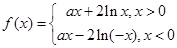 . 14分
. 14分
考点:1、含参数的一元二次不等式的解法;2、奇函数的解析式得求法.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 是定义在
是定义在 上的增函数,且
上的增函数,且
 的值;(2)、若
的值;(2)、若 ,解不等式
,解不等式 .
.
 的值,据此提出一个猜想,并予以证明;
的值,据此提出一个猜想,并予以证明; 的下方.
的下方. .
. 上画出函数
上画出函数 的图象 ;
的图象 ; . 试判断集合
. 试判断集合 和
和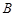 之间
之间 时,求证:在区间
时,求证:在区间 上,
上, 的图象位于函数
的图象位于函数
 .
.
 成立的
成立的 的取值范围;
的取值范围; ,
, ,求实数
,求实数 的取值范围.
的取值范围. 满足
满足 ,
,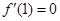 且
且 在
在 上恒成立.
上恒成立. 的值;
的值; ,解不等式
,解不等式 ;
; ,使函数
,使函数 在区间
在区间 上有最小值
上有最小值 ?若存在,请求出实数
?若存在,请求出实数 .
. 时,求曲线
时,求曲线 在原点处的切线方程;
在原点处的切线方程; 时,讨论函数
时,讨论函数 在区间
在区间 上的单调性;
上的单调性; 对任意
对任意 成立.
成立.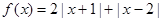 .
. 在每段区间上的解析式,并在图中的直角坐标系中作出函数
在每段区间上的解析式,并在图中的直角坐标系中作出函数 对任意的实数
对任意的实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 是奇函数,且当
是奇函数,且当 时,
时, ,求
,求 时,
时,