题目内容
已知抛物线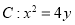 的焦点为
的焦点为 的准线和对称轴交于点
的准线和对称轴交于点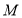 ,点
,点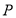 是
是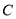 上一点, 且满足
上一点, 且满足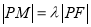 ,当
,当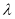 取最大值时,点
取最大值时,点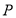 恰好在以
恰好在以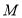 、
、 为焦点的双曲线上,则双曲线的离心率为 .
为焦点的双曲线上,则双曲线的离心率为 .
练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
题目内容
已知抛物线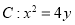 的焦点为
的焦点为 的准线和对称轴交于点
的准线和对称轴交于点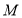 ,点
,点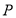 是
是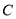 上一点, 且满足
上一点, 且满足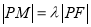 ,当
,当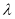 取最大值时,点
取最大值时,点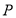 恰好在以
恰好在以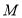 、
、 为焦点的双曲线上,则双曲线的离心率为 .
为焦点的双曲线上,则双曲线的离心率为 .
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案